ТЕОРИЯ сварочных процессов

Свойства металлов при температурах сварочного термического цикла

Особенность процесса образования деформаций и напряже­ний при сварке — изменение свойств металлов в шцроких пре­делах, обусловленное переменными температурами и характером развития деформаций.

Параметры упругости металлов, используемые в расчетах сварочных деформаций и напряжений (например, Е — нормаль­ный модуль упругости, G — модуль сдвига, К — объемный мо­дуль, v — коэффициент Пуассона), в малой степени зависят от
условий деформирования и могут определяться экспериментами при различных температурах, соответствующих сварочным. Ука­занные параметры упругости функционально связаны между со­бой так, что независимыми остаются два параметра из четырех. Известные экспериментальные данные показывают, что для целого ряда конструкционных материалов изменение коэффици­ента Пуассона при повышении температуры несущественно. По­этому рекомендуется в расчетах сварочных деформаций и напря­жений принимать коэффициент Пуассона v = const и равным значению его при нормальной температуре. Для эксперименталь­ного определения модуля сдвига проводят испытания на круче­ние тонкостенного трубчатого образца при постоянной темпера­туре с постоянной скоростью деформирования. Подобные испыта­ния проводят для ряда температур из диапазона сварочных с интервалом АГ = 50.. 100 К, начиная с нормальной температуры Го Диапазон сварочных температур для исследования деформа­ций и напряжений следует ограничить максимальной температу­рой Гк, при которой предел текучести материала близок к нулю. Для алюминиевых сплавов значение температуры Гк находится в диапазоне 573...673 К, для низкоуглеродистых сталей Гк = = 873 К, для коррозионно-стойких сталей и титановых сплавов Гк= 1073 .1173 К Зная коэффициент Пуассона v, и модуль сдви­га G„ можно подсчитать значения нормального модуля £, и объемного модуля Ki при соответствующей температура Г,:

Е,= 26.(1 + V,);

у 20.0 + У.) *11,6)

I — 2v,

Можно определить нормальный модуль Е, эксперименталь­но — растяжением образцов при постоянной температуре с пос­тоянной скоростью деформирования. Испытания также следует проводить для ряда температур из диапазона сварочных, а за­тем, используя формулы (116), подсчитать значения модуля сдвига G, и объемного модуля К,.

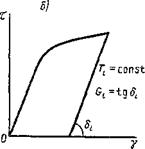
Следует отметить, что целесообразно при проведении экспе­риментов на кручение или растяжение подсчитывать модули при разгрузке, а не на стадии нагружения. При этом используется явление задержки ползучести при уменьшении напряжения, тог­да как на стадии нагружения возможны погрешности вследствие процесса ползучести (рис. 11.2). На рис. 11.3 представлены экспериментальные кривые зависимости нормального модуля упругости от температуры для ряда конструкционных матери­алов.

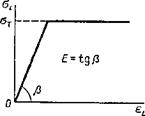
При исследованиях процессов образования временных и остаточных деформаций и напряжений важный фактор представ­ляет собой вид деформационной характеристики материала, вво­димой в расчет В большинстве случаев используют диаграмму идеального упругопластического материала (рис. 11.4), характе-

Рис 11 2 Кривые нагрузки — разгрузки образцов при дефор­мировании при постоянной температуре а — растяжение, б — кручение

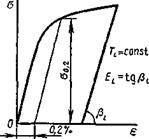
ризуемую значениями модуля упругости Е и предела текучести От материала. Применительно к низкоуглеродистым сталям по­добное упрощение не приводит к большим погрешностям, так как истинная диаграмма характеризуется наличием площадки текучести при протекании пластических деформаций до 3 4%. Максимальный уровень пластических деформаций при сварке, как правило, не превышает указанной величины. Для титановых и алюминиевых сплавов и для большинства легированных сталей площадка текучести на диаграмме нагружения материала отсут­ствует и при построении диаграммы идеального упругопластиче­ского материала условно принимают 0Т=0О2 (см. рис. 11.2). В этом случае схематизация в виде диаграммы идеального уп­ругопластического материала с условным пределом текучести приводит к погрешностям, так как пластическая деформация сопровождается упрочнением металла и повышением в нем на­пряжений выше условного предела текучести. На рис 11 5 для

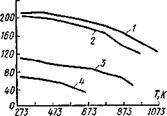
Рис 11 5 Зависимость предела теку­чести от температуры

I—коррозионно стойкая сталь 12 Х18Н10Т, 2 — низкоуглероднстая сталь. СтЗ, 3 — тех ническнй титан, 4 — алюминиевый сплав АМгб

Рис 116 Дилатограммы ма териалов при охлаждении об разное

І — сталь І2Х18Н10Т, 2 — сталь 20X13

ряда конструкционных материалов представлены кривые зависи­мости предела текучести от температуры, которые используются в диаграммах идеального упругопластического материала При выполнении приближенных расчетов используется схематизи­рованная зависимость предела текучести от температуры Так, в приближенных расчетах для низкоуглеродистой стали принима­ют, что в диапазоне температур от Т — 273 К до Т — 773 К предел текучести не зависит от температуры, а далее при повы­шении температуры до Т — 873 К уменьшается по линейному за­кону до нулевого значения.

Нагрев и охлаждение металлов вызывают изменение линей­ных размеров тела и его объема. Эта зависимость выражается через функцию свободных объемных изменений а, вызванных термическим воздействием и структурными или фазовыми пре­вращениями. Часто эту величину а называют коэффициентом линейного расширения. Значения коэффициентов а в условиях сварки следует определять дилатометрическим измерением. При этом на образце воспроизводят сварочный термический цикл и измеряют свободную температурную деформацию всв на неза­крепленном образце. Текущее значение коэффициента а пред­ставляют как тангенс угла наклона касательной к дилатометри­ческой кривой д&св/дТ. В тех случаях, когда полученная зави­симость Bed[Т) значительно отклоняется от прямолинейного за­кона, в расчет можно вводить среднее значение коэффициента Оср = tg6cp, определяемое углом наклона прямой линии (рис. 11.6, кривая 1). Если мгновенные значения а = дгсв/дТ на стадиях нагрева и охлаждения существенно изменяются при из­менении температуры, то целесообразно вводить в расчеты сварочных деформаций и напряжений переменные значения а, задавая функции а = а (Г) как для стадии нагрева, так и для ста­дии охлаждения. 4В

Однако в общем случае, когда возможны резкие изменения а от температуры вследствие фазовых превращений (рис. 11.6, кривая 2), представляется затруднительным подбор непрерывной функции. Проще аппроксимировать зависимость а = а(Т) кусоч­но-линейной функции. На каждом температурном интервале АТ, функция а, характеризуется средним значением

а, = tg0, = АєсвУД Т,.

При точных расчетах следует дилатограмму разбивать на ма­ленькие температурные участки с шагом АТ, = 20...30 К.

Расчеты сварочных деформаций и напряжений с использова­нием схематизированных диаграмм идеального упругопластиче­ского материала (см. рис. 11.4) или деформационных характе­ристик (см. рис. 11.2), полученных на основе изотермических испытаний образцов при постоянной скорости нагружения, сле­дует рассматривать как приближенные. Для количественной оцен­ки остаточных напряжений такие приближенные расчеты вполне достоверны и обеспечивают необходимую для практики точность.

При определении временных напряжений в процессе сварки приближенные расчеты с использованием схематизированных диаграмм материалов не обеспечивают высокой точности. Для повышения точности следует определять свойства металлов ис­пытаниями не с постоянной скоростью нагружения, а при вос­произведении термодеформационных сварочных циклов.