СОВРЕМЕННЫЕ СИСТЕМЫ УПРАВЛЕНИЯ
Понятие корневого годографа
Динамические свойства замкнутой системы управления определяются её передаточной функцией
|
(7.1) |
Y(s) p{s)
T(s) = -
Ris) qis)
|
(7.2) |
где p(s) и q(s) — полиномы относительно переменной s. Корни полинома q(s) определяют составляющие реакции системы. Для простой одноконтурной системы, изображённой на рис. 7.1, характеристическое уравнение имеет вид:
1 + KG(s) = О,
где К — варьируемый параметр. Корни характеристического уравнения системы в общем случае являются комплексными, поэтому (7.2) можно записать в ином виде:
|XC(s)| е' argM;(-') = -1 + jO. (7.3)
Следовательно, необходимо выполнение условий:
|
(7.4) |
|
|ХС(5)| = 1 |
avgKG(s) = 180° ± £360°,
|
= 0, |
|
или |
|
(7.5) |
|
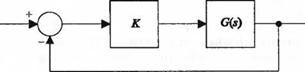
Рис. 7.1 Замкнутая система управления с варьируемым параметром К |
|
|
|
ад |
|
где к = 0, ±1, +2, ±3,... Корневой годограф — это траектории корней характеристического уравнения системы на s-плоскости при изменении какого-либо параметра системы. На рис. 7.2 изображена простая система второго порядка, которая рассматривалась нами в предыдущих главах. Характеристическое уравнение имеет вид: К |
|
sis+ 2) qis) = s2 +2s+K =s2 + 2Qans+ a2 =0. R(s) |
|
A(s)=l+A:G(s) = l+- |
|
Рис. 7.2 Система с обратной связью варьируемым параметром К |
|
r(s) |
единичной ~^ґ
вязью и
|
К |
1 |
|
|
s(s + 2) |
Траектории корней при изменении К находятся из условии:
К
|
(7.6) |
|
= 1 |
G(s) =
s(s+2)
arg G(s) = ± 180°, ±540°,... (7.7)
Коэффициент К может изменяться от 0 до со. Для системы второго порядка корни её характеристического уравнения
5] ,s2 = - С<ол ± шнл/с2 - І (7-8)
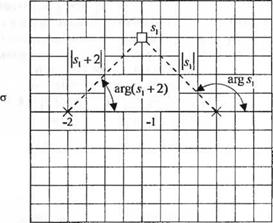
причём известно, что при С, < 1 arccos С, = 0. Как изображено графически на рис. 7.3, при £ < 1 траектории корней должны иметь вид вертикальной. линии, чтобы выполнялся угловой критерий (7.7). Например, как показано на рис. 7.4, для корня s,
arg ^ =-argj, - arg(sj +2) = —[(180° —0)+0] = -18О°. (7.9)
s(s+2)
Угловой критерий выполняется в любой точке вертикальной линии, перпендикулярной отрезку действительной оси от 0 до —2 и проходящей через его середину. Значение К, соответствующее точке 5[, можно найти с помощью выражения (7.6):
|
К |
|
(7.10) |
|
= 1, |
|
, ЫК+2| |
|
|
|
Рис. 7.3. Корневой годограф системы Рис. 7.4. Вычисление модуля и второго порядка для Кв < К < аргумента G (s) для точки при К = К |
|
к2 |
j(0 |
|||||||||||
|
Ув |
ели |
чен |
ие |
к |
||||||||
|
і |
||||||||||||
|
f1 |
||||||||||||
|
Д |
||||||||||||
|
ч |
ґ' |
'е |
f. |
'"і |
||||||||
|
2 |
L |
J |
1 = |
-Сс |
||||||||
|
Увеличение А 1 1 1 1 і |
||||||||||||
|
□ — полюсы |
||||||||||||
|
замкнутой системы X — полюсы разомкнут |
L |
pi |
||||||||||
|
г |
||||||||||||
|
□И |
Ц |
|||||||||||
|
і і і і і |
к2 |
|
5(5+2) |
|
К |
откуда
|
(7.11) |
К = |s,| К + 2|,
где 1^1 — модуль вектора, проведенного из начала координат в точку s,, a |s, + 2| — модуль вектора, начало которого находится в точке —2, а конец — в точке Sj.
|
|
Для многоконтурной системы в разделе 2.7 применение формулы Мейсона к сигнальному графу дало результат:
(7.12)
где Ltj есть коэффициент передачи q-го контура. Следовательно, мы можем записать характеристический полином в виде:
|
(7-13) (7.14) (7.15) |
|
q(s) = A(s) = 1 + F(s). Чтобы найти корни характеристического уравнения, приравняем (7.13) нулю: 1 + F(s) = 0. Последнее уравнение можно переписать в виде: F(s) = - 1 +J0 , |
и корни характеристического уравнения должны удовлетворять этому соотношению. В общем случае функцию F(s) можно представить в виде:
F(s)-K(s+Zi Хд + г2)(Д+^з)--(Д+^н,)
(s+ р{) (s+ р2 )(s + ръ )... (S+ р„ )
Тогда амплитудный и угловой критерий для корневого годографа принимают вид:
|
|5+£>1І|5+/Ь|... |
(7.16)
и
argF(s) =arg(s+ z, ) + arg(s+z2 )+...-arg(s + px )-arg(s+ p2 )-... = 180° ± g,360°,(7.17) где q — целое число. Амплитудный критерий (7.16) позволяет определить значение К, соответствующее определённому положению корня Sj. Принадлежность точки s, корневому годографу подтверждается, если выполняется условие (7.17). Все углы отсчитываются от горизонтальной линии против часовой стрелки.
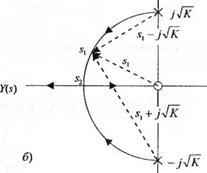
Теперь на примере системы второго порядка, изображённой на рис. 7.5 (о), мы покажем, как с помощью корневого годографа можно исследовать влияние варьируемого параметра а на свойства системы. Для этого характеристическое уравнение необходимо привести к такому виду, чтобы параметр а входил множителем в числитель соответствующего слагаемого. В данном случае исходное характеристическое уравнение имеет вид:
l+/£G(s) = 1н----- —— =0,
|
|
s2 + as + К — 0. Поделив это уравнение на (s2 + К), получим:
|
|
|
|
|
О |
|
ад- |
|
а=- |
|
я) Рис. 7.5. (а) Одноконтурная система, (б) Корневой годограф как функция параметра а Для корня s, амплитудный критерий выполняется, если =1 (7.19) 1*1 +*1 Угловой критерий имеет вид: args, — arg(s, + jy[K)-arg(sl - j-ІК ) = ±180°, ± 540°,... В принципе корневой годограф можно построить путём определения точек на s-плоскости, которые удовлетворяют угловому критерию. В следующем разделе мы опишем 12-этапную процедуру построения корневого годографа. На рис. 7.5 (б) изображён корневой годограф, соответствующий характеристическому уравнению (7.18). В частности, значение параметра а, соответствующее корню s1; определяется из (7.19): (720) l*i I Оба корня сходятся на действительной оси в точке s2, при этом реакция системы на ступенчатое воздействие является критически демпфированной. Корням s9 = а? соответствует значение параметра а, равное a2-jjK\c2+j-jK с+К |
|
G(s) |
||
|
К |
1 |
|
|
v(.v + а) |
|
(7.21) |
|
О 2 <?2 где а2 находится как длина векторов на s-плоскости, т. е. ст, = - JK. При дальнейшем увеличении параметра а оба корня являются действительными и различными, один из них больше, чем ст2, другой — меньше. Вообще говоря, желательно как-то упорядочить процедуру построения корневого годографа, сведя её к последовательности отдельных операций. Этим мы займемся в следующем разделе. |
|
Корни характеристического уравнения несут ценную информацию о поведении системы во времени. Здесь мы рассмотрим процедуру из двенадцати этапов, позволяющую быстро построить корневой годограф. |