ПРОЦЕССЫ ИНЖЕНЕРНОЙ ЗАЩИТЫ ОКРУЖАЮЩЕЙ СРЕДЫ

Свойства переноса в многокомпонентных системах

Процессы переноса теплоты, импульса и массы, обусловленные самопро­извольными перемещениями молекул, радикалов, атомов, ионов, имеющими в газах и жидкостях характер броуновского, а в твердых телах - колебатель­ного движения, протекают в направлении выравнивания температур, дав­лений и концентраций.

Согласно воззрениям молекулярно-кинетической теории интенсив­ность процессов переноса в газах и жидкостях однозначно определяется длиной свободного пробега частиц и, следовательно, их физико - химическими характеристиками и параметрами состояния. В зависимости от последних длина свободного пробега может изменяться в широких пре­делах, а в нормальных условиях она составляет порядка нескольких десятых долей микрометра. Так, средний свободный пробег молекул азота и кислорода в воздухе при обычных атмосферных условиях приблизительно равен (5.8)10 м.

Процесс распространения теплоты в покоящейся среде описывается уравнением Фурье:

Q/(Tf = - XdT/dn, (1.32)

Где X - коэффициент пропорциональности между плотностью теплового по­тока q/(tf) и градиентом температур dT/dn в направлении, нормальном к по­верхности, через которую проходит тепловой поток.

Коэфициент X в уравнении (1.32) носит название коэффициента теплопро­водности и численно равен величине теплового потока, проходящего через слой вещества единичной толщины и площади при единичной разности температур на его границах. Величина коэффициента теплопроводности газов и газовых смесей уменьшается с ростом их молекулярной массы и повышается с увеличением тем­пературы. Зависимость коэффициента теплопроводности от температуры при­ближенно выражается соотношением:

X t = X)[(273 + k)/(T + k)](T/273)3/2 Вт/(мК), (1.33)

Где k - эмпирическая константа, равная для азота 107, для кислорода 138, воз­духа 122, водяного пара 673, водорода 138, диоксида углерода 255, оксида углерода 102, метана 200, этана 300, пропана 320, бутана 340.

Коэффициенты теплопроводности смесей нереагирующих газов, близких к идеальному состоянию, можно подсчитать с допустимой для практических целей погрешностью по правилу аддитивности. Для двухфазных систем конденсацион­ных и диспергационных аэрозолей точные данные могут быть получены только опытным путем. Ориентировочно теплопроводности таких систем можно подсчитать как средневзвешенные величины по теплопроводностям твердой, жидкой и паровой фаз. Единицей измерения коэффициента теп­лопроводности в СИ является 1 Вт/(мК).

Плотность конвективного теплового потока при контакте движущейся жидкой или газообразной среды с непроницаемой поверхностью вычисля­ют по уравнению Ньютона-Рихмана:

Q/(tf) = а At, (1.34)

Где а - коэффициент теплоотдачи, Вт/(м С); At - разность температур между поверхностью и потоком, °С.

Значения коэффициентов теплоотдачи для конкретных случаев кон­вективного теплообмена определяются опытным путем и обобщаются в форме критериальных зависимостей.

При движении какого-либо тела в жидкости или в газе возникают си­лы, противодействующие этому, движению. Их называют силами сопро­тивления среды. Они вызваны тем, что движущееся тело увлекает за собой частицы жидкости и перемещает ее слои относительно друг друга. При этом возникают тормозящие силы, которые называются силами внутренне­го трения, или силами вязкости (вязкостью).

Ньютон показал, что для тонких слоев жидкости, находящихся на расстоянии Ax друг от друга и движущихся со скоростью v1 и v2, сила внутреннего трения S прямо пропорциональна градиенту скорости и пло­щади поверхностного слоя Af, т. е.

S = n(Av/Ax)Af (1.35)

Где п - коэффициент пропорциональности, получивший название коэффи­циента динамической вязкости среды.

2

Единица динамической вязкости равна 1 Н с/м, или Па с, т. е. вязкости

Такой жидкости, в которой 1 м слоя испытывает силу 1 Н при градиенте

2 11 скорости 1 м с/м. Размерность этой единицы м" кг с" . Прежняя единица

Измерения динамической вязкости (пуаз в системе СГС) равна 0,1 Н с/м.

Между перемещающимися частицами и слоями реальных газов или жидко­стей всегда возникает сила трения. Величина касательного напряжения, обу­словленная трением частиц друг о друга или об ограничивающие поверхности, по закону Ньютона пропорциональна градиенту скорости в направлении нор­мали к плоскости, ориентированной по течению:

S/f= - ndw/dn, (1.36)

2

Где S/f - сила, отнесенная к единице площади, Н/м (или Па); w - скорость потока, м/с.

Введено также понятие коэффициента кинематической вязкости v = п/р, (1.37)

Где р - плотность жидкости.

Единица коэффициента кинематической вязкости в системе СИ - м /с, с такой же размерностью. Прежняя единица измерения кинематической вязкости (стокс в системе СГС) имеет размерность см /с.

Вязкость среды зависит от температуры Т:

П = A'exp(EJRT), (1.38)

Где А - коэффициент пропорциональности, по физическому смыслу рав­ный вязкости среды при бесконечно высокой температуре; Еп - энергия активации процесса перемещения, в значительной степени зависящая от структуры жидкости.

Значение коэффициента динамической вязкости газов, как и значение коэф­фициента теплопроводности, уменьшается с увеличением молекулярной массы газов и газовых смесей и возрастает с температурой системы. Приближенно зави­симость коэффициента динамической вязкости газов от температуры можно вы­разить соотношением, аналогичным (1.33):

Пт = П0[(273 + k)/(T + k)](T/273)3/2 Пас. (1.39)

Наиболее точные значения коэффициентов вязкости газовых смесей и двухфазных систем могут быть получены эмпирически. Из расчетных зависи­мостей для смеси идеальных газов в инженерной практике нашла широкое употребление формула Гернинга и Ципперера:

П = ЪЦЯ (Пі Ткр І)1/2/2ГІ(ПІ Ткр i)1/2, (1.40)

Где ri - объемная доля i-го компонента; Ткрі - критическая температура i-го компонента.

Расчетные зависимости для двухфазных систем менее точны и могут использоваться наряду с аддитивными соотношениями, например, форму­лой Манна:

N

1/Vi = ЦГ/V), (1.41)

І = 1

Для грубой оценки величины вязкости в потоках.

Вязкость жидкости с повышением температуры снижается. У газов при их нагревании она возрастает, что указывает на различную природу внутреннего трения в газах и жидкостях. Главной причиной вязкости жид­кости являются силы взаимного притяжения молекул. Так как при нагре­вании она расширяется, то силы взаимного притяжения молекул в ней уменьшаются, поэтому вязкость снижается. Например, для воды при 0°С и 90°С п составляет соответственно 17,7510-4 и 3,2010-4 Нс/м2. Вязкость га­зов обусловлена переходом хаотически движущихся молекул из слоя в слой, которые при повышении температуры увеличиваются, и вязкость га­зов возрастает.

Вязкость жидкости в значительной степени определяет характер ее течения и истечения по трубам, из отверстий и в других случаях. При этом наибольшая скорость перемещения жидкости имеет место в центре потока, а наименьшая (нулевая) - у стенок трубы.

Различают два вида движения жидкой среды: установившееся (лами­нарное) и неустановившееся (турбулентное).

При ламинарном (слоистом) движении скорость течения жидкости в каждой точке пространства не изменяется со временем. В случае течения по цилиндрической трубе вся жидкость как бы разбивается на цилиндри­ческие слои, скорость которых вдоль трубы закономерно убывает по на­правлению от центра трубы к ее стенкам. Для ламинарного потока средняя скорость w^ движения жидкости равна половине максимальной ^макс ско­рости (в центре трубы), т. е. ^ср = 0,5 ^макс.

При турбулентном движении перемещение жидкости носит вихреоб - разный характер, а скорость ее течения в произвольной точке постоянно изменяется. Кривая распределения скоростей движения в турбулентном ядре потока имеет более пологий ход. Для турбулентного потока выполня­ется равенство w^ = 0,726 ^макс.

Ламинарные и турбулентные потоки могут превращаться один в дру­гой. Английский ученый Рейнольдс (1883 г.) показал, что характер движе­ния определяется величиной некоторого безразмерного комплекса, назван­ного критерием Рейнольдса Re. Он может быть выражен через различные величины. В частности, при обтекании твердого тела потоком жидкости

Re = wd/v, (1.42)

Где w - скорость обтекания; d - диаметр тела; v - коэффициент кинемати­ческой вязкости.

Для случая течения в трубах круглого сечения поток является лами­нарным при Re меньше 2100, при Re больше 2320 течение становится тур­булентным. Таким образом, турбулентность потока возрастает с увеличе­нием его скорости, размера обтекаемого тела и со снижением вязкости жидкости (газа).

Вязкостные характеристики жидкой и газообразной среды в значи­тельной степени определяют многие явления в технологических процес­сах. Величина вязкости среды существенно влияет на движение нефти и нефтепродуктов, природного газа и других материалов при перемещении их по трубопроводам. Они учитываются во всех остальных случаях, когда имеет место перемещение тела в той или иной жидкой или газовой среде.

Диффузия - процесс самопроизвольного перемещения вещества в про­странстве, ведущий к равномерному заполнению всего имеющегося объе­ма молекулами данного вещества и выравниванию его концентраций. Диффузия может осуществляться только тогда, когда в различных точках пространства концентрация вещества неодинакова. Движущей силой диф­фузии является градиент концентраций, т. е. их изменение в соседних уча­стках фазы.

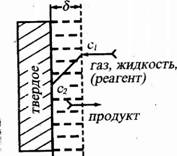
На рис. 1.6 представлена одна из схем диффузии (газа, жидкости к по­верхности твердой фазы), часто встречающаяся в технологических процес­сах. К поверхности твердого тела прилегает слой 5 жидкого или газообраз­ного реагента, в котором выравнивание концентраций во всех случаях происходит только за счет процесса молекулярной диффузии. В остальном объеме раствора их выравнивание может быть осуществлено конвективной диффузией (макродиффузией), например перемешиванием.

Чем интенсивнее перемешивание, тем меньше толщина 5 диффузион­ного слоя. Однако даже в турбулентном потоке у поверхности твердого те­ла остаются два тонких слоя: ламинарный и диффузионный. Через послед­ний осуществляется лишь молекулярная диффузия. Уменьшение толщины диффузионного слоя достигается не только увеличением скорости турбу­лентного потока, но и линейных размеров обтекаемого твердого тела. По­следнее в соответствии с выражением (1.12) способствует более интенсив­ной турбулизации потока. Толщина диффузионного слоя составляет обыч­но (0,02... 0,05) мм и менее.

С2 с,

Количество вещества dm, проходящего при диффузии через площадь S за время dt, пропорционально произведению площади, времени и гради­ента dc/dx концентрации С вещества по расстоянию х:

Dm = - DS(dc/dx)dt. (1.43)

Уравнение (1.43) известно как первый закон Фика (1855 г.). D - коэффициент диффузии, представляющий количество вещества, проходящего в единицу времени через единицу площади при градиенте концентрации, равном единице.

2

Обычная размерность для коэффициента диффузии - см /с. Его вели-

2 4 5

Чины составляют: для газов (0,1.1,0) см /с, для жидкости (10 10 ) 2 2 2 см. /с, для твердых тел 1 см /год.1 см /век.

Коэффициент диффузии в меньшей степени, чем константа скорости химической реакции, зависит от температуры. Он увеличивается в 1,1.1,5 раза при повышении температуры на 10°С.

Энергия активации диффузии не превышает 30 кДж/моль, т. е. также значительно меньше, чем энергия активации гомогенных химических ре­акций.

Процесс распространения молекул одного из компонентов в неподвижной

Газовой смеси также описывают уравнением Фика в другом виде, аналогичным

Уравнениям переноса теплоты и импульса:

M/(Tf = - D(dc/dn), (1.44)

Где D - коэффициент пропорциональности между плотностью потока массы. 2.

M/(if), кг/(м с) и градиентом концентрации dc/dn в направлении, нормаль-

3.

Ном к поверхностям постоянной концентрации, кг/(м м), называемый коэф­фициентом диффузии. В СИ он измеряется в м /с.

Зависимость коэффициента диффузии от температуры и давления при­ближенно можно выразить соотношением:

D = D 0(T/T)1,5 (p/p) м2/с. (1.45)

Коэффициенты диффузии определяют опытным путем. Эмпирические све­дения для отдельных газов приведены в приложении. При отсутствии опытных данных для двухкомпонентных газовых смесей с веществами А и В часто ис­пользуют полуэмпирическую формулу Джиллиленда:

Dr = 4,35 1 08T1,5[(1/Ma)+ 1/Mb)]1/2/(p[(106Va)1/3+(106vb)1/3]2} м2/с, (1.46) где р - абсолютное давление в системе, МПа; vA и vB - мольные объемы газов А и В, м /моль; МА и Мв - молекулярные массы газов А и В.

Вычислять коэффициенты диффузии для двухкомпонентных газовых смесей можно также по более точной формуле Чен Нинг Хсинго и Омара:

Dr = 0,15110-5(T/100)1,81[(1/M )+(1/Mb )]1/2/(P[(104Va)0,4+(104Vb)0,4]2x

Х(10-4ТА. кр Тв. кр)0,14} м2/с. (1.47)

Коэффициент диффузии молекул газа А, растворенных в жидкости В, мож­но подсчитать ориентировочно по выражению:

D-ж = 106[(1/M )+(1/M* )]1/2[1+0,2пж1/2(^-20)/рж]/ (сПж1/2[(106^)1/3+(106Ув)1/3]2},

(1.48)

Где пж - коэффициент динамической вязкости чистой жидкости В при 20°С, мПа с; t - температура раствора, °С; с - коэффициент, зависящий от ассоциированности молекул раствора, который можно принимать: для неас - социированных жидкостей (бензол, эфиры) 1; для ацетона 1,15; для спиртов 2; для воды 4,7.

Коэффициенты диффузии веществ в разбавленных растворах приближенно можно подсчитать по формуле:

Dж = 7,410-12(c1M)0,577M106'v)0,6], (1.49)

Где М - мольная масса растворителя; v - молекулярный объем растворенного газа, м3/моль; Т - температура раствора, К; c1 - коэффициент, который можно принимать: для неассоциированных жидкостей 1; для спиртов 1,5; для воды 2,6.

Коэффициент диффузии газа в жидкости Dt (при температуре t) связан с коэффициентом диффузии D2o (при температуре 20°С) следующей при­ближенной зависимостью:

Dt = D2o[1 + b(t - 20)], (1.50)

В которой температурный коэффициент может быть определен по эмпири­ческой формуле

B = 0,2'пШрШ, (151)

Где n - динамический коэффициент вязкости жидкости при 20°С, мПа; р - плотность жидкости, кг/м3.

В движущейся многокомпонентной газовой среде плотность конвективного потока массы определяется по соотношению, аналогичному уравнению Ньюто- на-Рихмана:

M/(xf = РАС, кг/(м2с), (1.52)

Где Р - коэффициент массоотдачи, м/с; АС - разность концентраций диффундирующего вещества в потоке, кг/м.

Значения коэффициентов массоотдачи для конкретных процессов массо - обмена определяются опытным путем и обобщаются в форме критериальных зависимостей.

В неподвижных аэродисперсных системах может происходить диффузионное распространение взвешенных частиц размером менее 1 мкм. Такие частицы со­вершают хаотичные перемещения наподобие броуновского движения молекул, но с меньшей интенсивностью. Диффузия частиц является следствием их столкно­вений с молекулами, однако происходит значительно медленнее, чем диффузия молекул в газе. Коэффициенты диффузии частиц могут быть сравнимы по по­рядку с коэфициентами диффузии молекул в жидких растворах и изменяются

11 7 2

Ориентировочно в пределах 310 ...310 м /с для частиц размерами соответствен­но от 10-6 до 10-8 м. Коэффициент диффузии частиц D приближенно можно под­считать по формуле:

D = RTCJQ яп^рЯ), (1.53)

Где d^ - средний диаметр частиц, м; N - число Авогадро; Ск - число Кан - нингхема.

Число Каннингхема вводится в формулу (1.53) для учета проскальзы­вания частиц относительно молекул. Для частиц, взвешенных в воздухе при атмосферном давлении, его можно определить по упрощенному соотноше­нию:

СК = 1 + (6,210-7Шср). (1.54)

В потоках аэрозолей движение взвешенных частиц разных размеров имеет различный характер. Если режим движения потока ламинарный, а размеры час-

-7

Тиц соизмеримы с длиной свободного пробега молекул (ориентировочно 10- м и менее), то на их движении существенно сказываются диффузионные процессы.

Характер движения частиц, размеры которых превосходят длину свободного пробега молекул, в основном определяются силами, формирующими поток аэ­розоля (инерционными, гравитационными, электрическими и т. д.) и сопротив­лением среды.

Диапазоны размеров, в которых реализуются различные режимы движения частиц, устанавливают по критерию (числу) Кнудсена (Kn):

Kn = 2 /Jd4, (1.55)

Где /мг - средняя длина пробега молекул газа при заданных параметрах со­стояния, dH - диаметр частицы, причем обе величины выражают в одинаковых единицах измерения.

Если Kn > 0,1 при размерах взвешенных частиц менее 10-6 м, аэрозоль может рассматриваться как дискретная среда, взвешенные частицы которой пере­двигаются в пространстве между молекулами газа-носителя. При этом раз­личают 3 модели перемещения частиц: движение со скольжением (0,1< Kn< 0,3), переходное (0,3 <Kn< 10) и броуновское или свободномолекулярное (Kn >10).

При размерах частиц более 10-6 м поправкой Каннингхема пренебрега­ют, среду рассматривают как сплошную, а режим движения частиц назы­вают гидродинамическим или стоксовским. В качестве характеристики движения одиночной частицы в сплошном газовом потоке принимают для нее критерий Рейнольдса Re^ который подсчитывают по соотношению:

Яеч = dH - w г)/г|г, (1.56)

Где фг - объемная доля газа в потоке; wH, w г - скорости частицы и газа- носителя.

Обычно число ReH для твердых взвешенных частиц в пылегазовых выбро-

42

Сах имеет величину порядка 10' ...10 .

При проектировании пылегазоочистных устройств размеры частиц загряз­нителей характеризуют также числом (параметром) Стокса, который подсчиты­вают как отношение диаметра частицы или расстояния между частицами к харак­терному размеру l канала, в котором перемещается аэрозоль:

Stk = djl. (1.57)

Скорость частицы в потоке может меняться вследствие изменения вели­чины и направления действующих на нее сил. Характеристикой интенсивности изменения скорости частиц в таких случаях служит время релаксации т :

Т = ^ЧХр2рчСк/(18 Пг), (1.58)

T

Где коэффициент Каннингхема C к учитывают, если средний диаметр час­тиц аэрозоля ^ч. ср меньше 1 мкм.

Изменение направления и скорости потока аэрозоля при обтекании пре­пятствий часто используется для отделения взвешенных частиц от газа - носителя. Молекулы газа, огибая препятствие, образуют линии тока, расхо­дящиеся перед препятствием и смыкающиеся за ним. Параметры обтекания определяются в основном гидродинамическим режимом потока и геомет­рическими характеристиками препятствия. Характер перемещения взве­шенных частиц в значительной степени зависит и от их размеров.

Мелкие частицы (ориентировочно Kn > 1) огибают препятствие по линии тока вместе с молекулами. Если они проходят от препятствия на расстоянии не более длины свободного пробега, то под ударами молекул могут сойти с ли­нии тока и достичь поверхности препятствия. Для характеристики переноса взвешенных частиц на препятствие используют безразмерные числа Рейнольдса относительно препятствия (Яепр) и Шмидта (Sc):

Яепр = ^рг^пр/л г, (1.59)

Sc = л/(р D (1. 60

Где dnp - диаметр препятствия, м; D - коэффициент диффузии частиц, м /с.

Числа Re^, обычно изменяются в пределах 10-1...104, числа Sc - в пределах 102...106.

Частицы с числом Kn < 0,5 практически не ощущают столкновений с моле­кулами. Их движение в потоке зависит от соотношения сил инерции и сопро­тивления воздуха (без учета влияния гравитационных, электрических и других силовых полей), характеризуемого инерционным параметром частицы Мч: Мч = Скрч^2м//(9 л гd пр). (1.61)

Величину М^dпp можно интерпретировать как тормозной путь части­цы диаметром d4 и плотностью рч, имевшей начальную скорость w, в не­подвижной газовой среде с вязкостью Лг при отсутствии каких-либо воз­действий на частицу, кроме силы сопротивления газа. Параметр Мч может рассматриваться и как число Стокса, характеризующее процесс огибания частицей препятствия.

Частицы с инерционным параметром Мч > 0,08 (ориентировочная ве­личина) не могут обходить препятствие вместе с молекулами газа и про­должают движение в прежнем направлении. Сходя с линии тока, они стал­киваются с препятствием и захватываются им.

При небольших числах Re^ (ориентировочно Renp < l) течение потока около препятствия определяется вязкостью. Возмущения, создаваемые препятствием, передаются на расстояния, соизмеримые с его радиусом, и линии тока плавно оги­бают препятствие. Такое течение называют вязким.

При больших числах Re^ (ориентировочно Re^ > 500) режим обтекания препятствия становится потенциальным (невязким). Это означает, что вязкий подслой остается только в области, непосредственно прилегающей к поверх­ности препятствия, и возмущения от препятствия не передаются в более от­даленные области потока. Поэтому линии тока расходятся, круто изгибаясь в непосредственной близости к препятствию.

Влияние сил инерции на осаждение частиц в потенциальном потоке значительно выше, чем в вязком.

Частицы любых размеров могут быть захвачены препятствием, даже оги­бая его по линии тока, если поверхности частицы и препятствия соприкоснут­ся. Это явление может произойти тогда, когда линия тока удалена от поверхно­сти препятствия не более чем на радиус частицы. Улавливание частиц вследст­вие их касания препятствия характеризуется параметром перекрывания (ка­сания, зацепления):

Ашс = d^d^. (1.62)