Основы ТЕХНОЛОГИИ МАШИНОСТРОЕНИЯ
ЯВЛЕНИЕ РАССЕЯНИЯ ВЫХОДНЫХ ПОКАЗАТЕЛЕЙ ТЕХНОЛОГИЧЕСКОГО ПРОЦЕССА
В ходе технологического процесса непрерывно изменяются качест - иенные характеристики технологической системы, действующие факторы, характеристики заготовок и деталей, поступающих на вход технологической системы, и др. Все это в итоге приводит к появлению отклонений качества изготовленного изделия, затрат времени на его изготовление и себестоимости от заданных значений.
Если, например, обработать партию деталей на станке и измерить размер каждой детали, то все они будут иметь разные размеры. Совпадение размеров у двух деталей объясняется погрешностями измерения. Ес - 1111 же произвести измерение с большей точностью, то удастся уловить разницу между этими размерами. Описанное явление получило название пиления рассеяния.
При изучении явления рассеяния характеристик технологических процессов получили распространение две формы графического отображения этого явления: точечная диаграмма и кривая рассеяния.
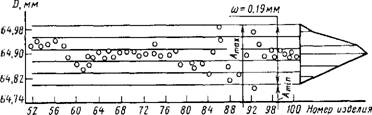
Точечная диаграмма строится следующим образом. По оси ординат о! кладываются значения выходного показателя, по оси абсцисс - номер изделия (рис. 1.5.3). Преимущество такой формы отображения явления рассеяния заключается в возможности наблюдения динамики изменения иыходного показателя.
|
Гие. 1.5.3. Точечная диаграмма изменения диаметра в партии деталей |
Построение кривой рассеяния осуществляется следующим образом. Па точечной диаграмме через Amas и Атш значения выходного показателя проводят линии, параллельные оси абсцисс и делят расстояние между ними на п одинаковых интервалов. Из середин интервалов восстанавливают перпендикуляры к линии, проведенной параллельно оси ординат, и на каждом перпендикуляре откладывают отрезок, пропорциональный количеству значений выходного показателя, попавших в данный интервал. Соединив концы отрезками в виде ломаной линии, получим фактическую кривую рассеяния выходного показателя технологического процесса. Если количество интервалов будет бесконечно большой величиной, то получим плавную кривую рассеяния.
Для количественной оценки рассеяния выходных показателей пользуются характеристиками математической статистики и теории вероятностей. Основной числовой характеристикой является величина поля рассеяния си = А„шх - Ami„ (здесь А - значение выходного показателя).
К другим характеристикам кривой рассеяния относятся ее форма, центр группирования случайной величины и мера рассеяния характеристики относительно центра группирования.
Под центром группирования понимается среднее значение случайной величины, около которой группируются остальные ее значения. Если случайная величина дискретна, то центр группирования
М(х) =YdXip(xl),
Где х, - значение ;'-го интервала; р(х,) - частость или число значений случайной величины, попавших в один интервал, %. Если случайная вели чина непрерывна, то
|
|
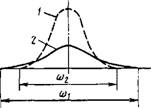
Однако знание положения центра группирования недостаточно для оценки кривой рассеяния выходного показателя. При одном и том же значении центра группирования кривые рассеяния могут иметь различную форму (рис. 1.5.4). В этом случае чтобы оценить различие кривых рассеяния, необходимо определить их меры рассеяния. Мера рассеяния дает представление о том, как плотно значения случайной величины группируются вокруг центра группирования.
За меру рассеяния отклонений случайной величины относительно центра группирования принимают среднее отклонение; среднее квадратическое отклонение; срединное (вероятное) отклонение; дисперсию, медиану и другие. Часто для упрощения расчетов в качестве меры рассеяния используют среднее квадратическое отклонение а.
Для дискретной случайной величины х
Для непрерывной случайной величины,
Чем больше а, тем менее плотно группируются значения случайной неличины относительно центра группирования.
Как правило, при большом числе изделий в партии больше вероятность того, что рассеяние значений выходного показателя будет подчиняться нормальному закону распределения (закону Гаусса). В этом случае, если поле рассеяния ш ограничить величиной, равной 6а, то число шачений выходного показателя, вышедших за пределы 6а, составит 0,27 %.
|
Рис. 1.5.4. Кривые рассеяния случайной величины: / — со! = боь 2- со, =6а2; а, < а2 |
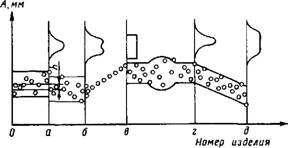
В реальных условиях фактические кривые рассеяния, как правило, оміичаются от кривой нормального распределения, нередко очень существенно. Объясняется это тем, что факторы, вызывающие отклонения выходного показателя, значительно отличаются один от другого по величине и степени воздействия. Рассмотрим некоторые характерные случаи. Па рис. 1.5.5 видно, что на участке 0-а в результате действия многочис - иснных факторов рассеяние полученного размера А подчиняется закону нормального распределения, а на участке а - б точечная диаграмма і мпцена на величину h, что обусловлено действием систематического ф. ииора, постоянного по величине (примером может служить процесс
|
Рис. 1.5.5. Точечные диаграммы, отражающие действия различных факторов |
Развертывания отверстий в деталях, когда сломанную развертку заменяют новой, имеющей другой фактический диаметр). Если для выборки 0-б построить кривую рассеяния, то она будет иметь "двугорбый" вид. На участке 6-е наблюдается систематическое изменение размера, близкое к линейному (примером является действие изнашивания шлифовального круга). Кривые рассеяния для выборки на участке 6-е будут подчиняться закону равной вероятности. Для участка в-г характерно влияние доминирующего случайного фактора (например, если среди заготовок оказалась партия заготовок, полученных на другом, уже изношенном штампе, имеющем большие размеры, то эта партия заготовок будет иметь больший разброс припуска), а кривая рассеяния будет близка к закону нормального распределения.
Изменения на участке г-д, обусловленные совокупным действием случайных факторов и одного систематического, подчиняющегося линейному закону, будут иметь кривую рассеяния размера, близкую по форме к трапеции.
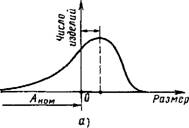
Для определенных условий технологического процесса, например при обработке партии деталей на станке, рабочий, чтобы не допустить неисправимый брак, старается уменьшить вероятность выхода размера детали за нижнюю границу допуска. В этом случае кривая рассеяния размера получается в виде асимметричной кривой с центром группирования, смещенным в сторону верхней границы допуска на размер (рис. 1.5.6, а).
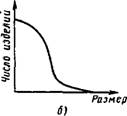
Кривая рассеяния какой-либо характеристики, являющейся положительной величиной (например, эксцентриситет), при действующих случайных факторах имеет вид кривой нормального распределения, расположенной в квадрате положительных значений (рис. 1.5.6, б).
|
Рис. 1.5.6. Кривые рассеяния: А - при стремлении рабочего не допустить неисправимый брак; б - положительной величины |
При длительном времени действия технологического процесса факторы, влияющие на него, изменяются по составу, величине и направлению. То один, то другой фактор в течение какого-то времени может стать доминирующим, поэтому в общем случае распределение выходных показателей технологического процесса во времени непрерывно изменяется.
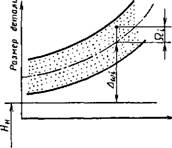
Отклонение выходного показателя технологического процесса для конкретного /-го изделия (рис. 1.5.7), равно алгебраической сумме отклонений, вызванных действием каждого фактора, т. е.
|
Номер детали |
|
Рис. 1.5.7. Схема базирования размера /-го изделия |
Н, = Нн + Д со, + Q„
Где Ни - номинальное значение выходного показателя; Да)/ - отклонение mo изделия, обусловленное совокупным действием систематических факторов; Q, - отклонение /-го изделия, обусловленное совокупным действием случайных факторов.
|
|
К основным числовым характери - сіикам рассеяния выходного показате - II» технологического процесса при изготовлении партии изделий относят поле рассеяния ш, координату Дш середины поля рассеяния, координату М(х) центра группирования, параметры, чирактеризующие кривую рассеяния (греднеквадратическое отклонение, шкперсию, коэффициент относительной асимметрии, медиану и др.).