Основы ТЕХНОЛОГИИ МАШИНОСТРОЕНИЯ
ОБРАЗОВАНИЕ ПОГРЕШНОСТЕЙ ИЗМЕРЕНИЯ
Вопросы измерения точности детали играют чрезвычайно важную роль в достижении заданной точности как детали, так и изделия в целом в процессе изготовления. Ошибки в измерении погрешностей изготов ленного изделия могут иметь существенные негативные последствия Например, неправильная оценка погрешности обработки детали приво дит к статической и динамической погрешностям настройки технологи ческой системы, неправильному назначению допусков на межперехол ные размеры и т. д.
|
|
|
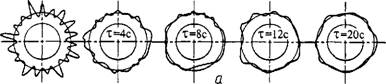
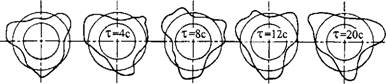
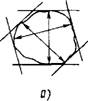
5 Рис. 1.6.40. Круглограммы поперечного сечения деталей после суперфиниширования |
Проблема оценки точности изделия с точки зрения соответствия ею служебному назначению является комплексной, когда должен учити
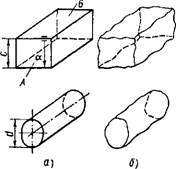
Рис. 1.6.41. Детали с идеальными поверхностями (а) и реальными поверхностями (&)
Ваться целый набор его характеристик с учетом их взаимосвязей. Вопрос этой очень сложен, недостаточно изучен и разработан, в связи с чем не представляется возможным дать его полное изложение.
Учитывая все же большую важность и актуальность проблемы в связи с непрерывным ростом требований к качеству изделий, рассмотрим на примере геометрической точности детали задачи, с которыми приходится сталкиваться при ее измерении.
Главной причиной, порождающей основные трудности в измерении геометрической точности изделия, является отличие формы реальных поверхностей от заданных на чертеже их геометрических прототипов. При конструировании машины, механизма, детали конструктор оперирует образами идеальных поверхностей и их сочетанием. Под идеальными поверхностями понимаются поверхности, заданные конструктором, например, плоскость, круговой цилиндр, винтовая поверхность и т. п. Однако у реальных деталей форма поверхности всегда отличается от заданной конструктором, это и приводит к трудностям в измерении точности. В качестве примера на рис. 1.6.41 показаны детали с идеальными (рис. 1.6.41, а) и реальными (рис. 1.6.41, б) поверхностями. Когда поверхности соответствуют заданным геометрическим образам, то легко, например, измерить расстояние с, диаметральный размер d, отклонение от параллельности а. У деталей с реальными поверхностями возникает проблема определения этих характеристик.
|
|
Отклонение формы реальных поверхностей от заданных привело к введению дополнительных геометрических характеристик, таких как отклонения от плоскостности, прямолинейности, цилиндричности, круглости (элементами которой являются овальность, огранка), откло
нение профиля в продольном сечении (конусообразность, бочкообраї ность, седпообразность, изогнутость) и др.
Введение этих характеристик усложнило методику измерения за счет таких дополнительных этапов, как определение положения базы отсчета и выбора критерия отклонения данной геометрической характеристики. Например, чтобы определить отклонение от параллельности поверхности Б относительно поверхности А (см. рис. 1.6.41), надо провести прилегающие плоскости к каждой из этих поверхностей.
Другой причиной повышенной трудоемкости процесса измерения точности машины является наличие многочисленных геометрических характеристик, отклонения которых надо измерять. К ним относятся от клонение от параллельности, биение, отклонение от перпендикулярности, перекос осей, отклонения от соосности, симметричности, перекрещивания осей и др.
В зависимости от типа контролируемого изделия появляются дополнительные геометрические характеристики, учитывающие его специфику. Например, при контроле точности зубчатого колеса измеряют погрешности шага между зубьями, накопленную ошибку шага, толщин} зуба и его направление. При этом каждая из геометрических характеристик требует своего метода и средств измерения.
Наличие такого многообразия геометрических характеристик привело к появлению множества методов и средств измерения, и тем самым повысило трудоемкость и стоимость измерений. Поэтому одной из важнейших задач совершенствования процесса измерения является унификация геометрических характеристик. Сокращение разнообразия геометри ческих характеристик позволит существенно повысить точность и эффективность процесса измерения.
Большой резерв в повышении эффективности и качества процесса измерения точности машин заложен в совершенствовании методов измерения. В ряде случаев наблюдается такой парадокс, когда преимущества высокоточных измерительных средств "сводятся на нет" недостатками методов измерения, т. е. погрешности измерения, вносимые методикой измерения, оказываются значительно выше погрешностей средств измерения. Одной из главных причин такого несоответствия является мно гоступенчатость процесса измерения, что приводит к накоплению по грешностей.
Все разнообразие методов измерения точности деталей и машин можно свести к двум принципиально отличным видам: комплексному и дифференцированному.
Сущность комплексного метода заключается в получении непосредственно в результате измерения ответа о годности или непригодности контролируемого объекта выполнять свои служебные функции (типичным примером такого метода является измерение с помощью проходного и не проходного калибров). Кроме того, в процессе измерения непосредственно можно контролировать и показатели служебного назначения объекта (например, при контроле плунжерной пары измеряют объем утечки рабочей среды за единицу времени и таким образом определяют годность этой плунжерной пары).
Преимуществом комплексного метода является возможность установления непосредственной связи между геометрией измеряемого объекта и его служебными функциями, а также отсутствие необходимости измерения многочисленных геометрических характеристик.
Таким образом, с точки зрения объема измерений, а следовательно, и потенциально меньшей погрешности измерения комплексный метод более предпочтителен. Однако его применение наталкивается на ряд таких трудностей, как недостаточное знание явлений, которые имеют место при выполнении изделием служебных функций. Другим недостатком комплексного метода является отсутствие информации об отклонениях геометрических характеристик, что затрудняет совершенствование технологии изготовления изделия и восстановление точности, теряемой в процессе эксплуатации.
В связи с указанными недостатками комплексного метода широкое распространение приобрел дифференцированный метод, сущность которого заключается в измерении отклонений группы геометрических характеристик.
Рассмотрим в качестве примера контроль точности вала. Точность детали оценивается комплексом показателей: точностью размера или расстояния между поверхностями, точностью относительных поворотов поверхностей и точностью геометрической формы поверхностей.
Упрощая задачу, рассмотрим только измерение точности вала в поперечном се чении. Для решения этой задачи надо изме рить сначала погрешность формы диамеї рального размера, а затем положение кои тролируемого сечения относительно опорных шеек вала (рис. 1.6.42).
В свою очередь, чтобы определитI. указанные погрешности, необходимо у ре ального вала (рис. 1.6.42, б) найти базы о і счета положения контролируемого сечения относительно опорных шеек. В качестве таких баз (согласно ГОСТ 24642-81) при мем оси этих шеек, а в качестве характери стики, определяющей погрешность положения поперечного сечения, ра диальное биение.
Исходной информацией для определения точности поперечного сечения вала являются результаты измерения фактических поверхно стей опорных шеек и профиля контролируемого поперечного сечения Поскольку поверхность шейки вала можно представить совокупностью профилей поперечного сечения, то для получения исходной информа ции надо определить п профилей поперечных сечений. Измерение точно сти профиля поперечного сечения осуществляют в несколько этапов.
Этап 1 - измерение профиля поперечного сечения вала, которое осуществляется различными способами. Наибольшее распространение на практике нашли три способа: двухконтактный, трехконтактный и измерение радиус-вектора (метод образцового вращения).
|
Б) Рис. 1.6.42. Ступенчатый вал с поверхностями: А - идеальными; б-реальными |
Двухконтактный способ измерения профиля детали заключается в измерении диаметрального размера сечения в разных направлениях. Под диаметральным размером профиля произвольной формы, отличающегося от окружности, понимается расстояние, заключенное между точками касания профиля с двумя параллельными прямыми. В общем случае диаметральные размеры не пересекаются в одной точке (рис. 1.6.43, а), поэтому по колебанию диаметрального размера нельзя судить о форме профиля детали. Например, в математике известна группа фигур, имею щих постоянную ширину, которые, резко отличаясь по форме, характерны
|
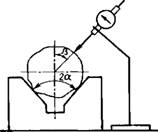
Рис. 1.6.43. Измерение профиля поперечного сечения: А - двухконтактным методом; б - трехконтактным методом |
Тем, что две любые параллельные опорные прямые удалены одна от другой на одно и то же постоянное для всех направлений расстояние. Примером такой фигуры является огранка с нечетным числом граней. Следовательно, при высоких требованиях к точности формы этот способ для измерения профиля не рекомендуется.
Трехконтактный способ измерения профиля детали обычно реализуется в виде измерения детали на призме (рис. 1.6.43, б). Результаты пока - іаний измерительного прибора при таком способе измерения зависят от формы измеряемого сечения, угла призмы 2а и угла р, заключенного между-биссектрисой угла и направлением измерения. Для определения но результатам измерений действительного профиля детали разработаны коэффициенты воспроизведения, определяющие связь между показаниями измерительного прибора и действительного профиля. Значения коэффициентов зависят от углов а и р и формы детали (рассматриваемой как ючетание гармоник, полученных после разложения уравнения профиля в ряд Фурье). Следует отметить, что углы аир определяют, какие номера і армоник будут обнаружены при таком сочетании параметров измерения, л па какие прибор не будет реагировать.
|
|
Таким образом, чтобы выявить трехконтактным методом все состав - пиющие гармоники профиля детали и определить действительный профіті, детали, необходимо производить измерения детали при различных комбинациях значений углов а и Р с последующим пересчетом. Такой > пособ трудоемок и не отличается высокой точностью. Определение
Формы детали путем измерения радиус - вектора (рис. 1.6.44) осуществляется при относительном вращении детали и измерительного устройства. В этом случае на точности измерения не сказывается характер измеряемой формы профиля, как это имело место в ранее рассмотренных способах. Однако схемы измерения, реализующие этот способ, вносят существенные погрешности.
Широко распространенной схемой измерения является измерение радиус - вектора детали при вращении ее в центрах. Измерительное устройство по такой схеме показывает отклонение от заданной величины, определяемое колебанием радиус-вектора профиля, смещением профиля относительно центров и отклонением от вращательного движения. Другие схемы измерения радиус-вектора, например, когда вращается измерительное устройство или деталь, имеют тот же недостаток - на погрешность измерения влияет отклонение от вращательного движения. Отсюда следует, что по радиальному биению нельзя судить о форме детали. Например, деталь имеет в сечении окружность, но так как невозможно без погрешности совместить центр окружности с центрами, то при измерении будет иметь место отклонение радиус- вектора, хотя в действительности погрешность формы отсутствует. Нередко и неточность вращательного движения познают (без каких-либо дополнительных пересчетов) через радиальное биение. Это приводит к неправильной оценке отклонения действительного движения от заданного. Возможен даже такой случай, когда неточность вращательного движения в сумме с погрешностью формы из-за разных знаков погрешности приведет к тому, что измерение покажет отсутствие радиального биения.
|
7777777777,' Рис. 1.6.44. Измерение радиус - вектора профиля поперечного сечения |
Допуская, что деталь совершает вращательное движение, идеализм руют явление и вводят такие понятия, как ось вращения, центр вращения, принимаемые во многих случаях в качестве измерительных баз, что при водит при измерении высокоточных деталей к серьезным ошибкам В действительности фактическое движение детали является сложным, .і не вращательным. Указанное допущение объясняется тем, что ранее и
подавляющем большинстве случаев при обработке деталей на станках точность формы получалась на один-два порядка выше точности размера. ')то и вызвало подмену на практике понятия сложного движения вращательным и, как следствие, выбор в качестве измерительных баз осей или центров вращения. В случае измерения высокоточных деталей указанного разрыва уже нет, и рассмотренные выше допущения становятся тормозом в достижении требуемой точности деталей.
Из рассмотренных выше способов измерения профиля поперечного сечения деталей предпочтительным является способ, основанный на измерении радиус-вектора профиля. Основной причиной, снижающей точность измерения по этому способу, является отклонение фактического движения детали от вращательного. Для сокращения этой погрешности следует не только совершенствовать конструкции известных приборов, но и разрабатывать принципиально новые методы и средства измерения.
Этап 2 - отображение результатов измерения профиля детали. После измерения профиля сечения для определения его погрешностей нужно в той или иной форме представить результаты измерения. Их можно изобразить в табличной или графической форме. Последняя более наглядна и позволяет визуально оценить отклонения профиля. Кроме того, при графическом способе легче анализировать характер погрешности, что особенно важно при анализе причин, порождающих погрешность.
|
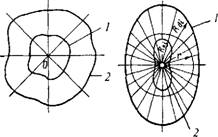
Рис. 1.6.45. Построение круглограммы: А - по абсолютным значениям радиус-вектора; б - по отклонениям радиус-вектора; / - кривые профиля: 2 - кривые круглограммы |
|
А) б) |
На практике наибольшее распространение нашло отображение формы круглых деталей в виде круглограммы или развертки. Круглограмма может быть построена по значениям модуля радиус-вектора или по отклонениям модуля радиус-вектора. Последний случай наиболее распространен из-за малой площади занимаемой круглограммы.
Сущность построения круглограммы по величинам радиус-вектора заключается в следующем. Пусть задана замкнутая кривая, являющаяся профилем (рис. 1.6.45, а). Необходимо построить круглограмму этой кривой большего масштаба. Тогда в области, ограниченной кривой, произвольно выбирают центр О и из него проводят лучи, на которых откладывают значения модуля радиус-вектора в требуемом масштабе, в ре зультате получаем фигуру, подобную замкнутой кривой. Условие подо бия обеспечивается тем, что каждый радиус круглограммы равен произведению радиуса детали на этом же луче на один и тот же масштабным коэффициент Кы.
К недостаткам этого способа отображения формы детали относится необходимость большой площади для построения круглограммы при не значительном увеличении, поэтому этот способ не нашел широкого при менения на практике.
|
(1.6.10) |
При построении круглограммы по отклонениям модуля радиус вектора масштабный коэффициент умножается на значение отклонения модуля радиуса за вычетом постоянной величины (рис. 1.6.45, б). При таком методе построения круглограммы нарушается условие подобия Действительно, радиус круглограммы на і-м луче
Як; - (Кщ - г) К
Где Лд, - радиус детали в і-м направлении; г - радиус окружности, вписанной в профиль; Км - масштабный коэффициент.
|
|
Поскольку из каждого радиуса детали, отличающегося друг от друга, вычитается постоянная величина, а не величина, пропорциональная каждому радиусу, происходит нарушение условия подобия, что приводи: к отличию профиля, записанного в виде круглограммы, от фактического Приращение радиуса круглограммы, обусловленное нарушением условия подобия, определяется из равенства
(1.6.11)
Из (1.6.10) следует, что отклонение радиуса круглограммы от радиу са, соответствующего условию подобия, тем больше, чем больше Км, Г н чем больше отношение Ru/ Дд, отличается от единицы. Формула (1.6.10) показывает, что если записать две круглограммы одного и того же про
филя, но от разных центров профиля, то круглограммы будут иметь разную форму. Действительно, согласно формуле (1.6.10), при различных центрах отсчета радиуса отношение Ra, /Лд) будет различное, следова - іельно, и ошибки радиусов круглограммы, вызванные нарушением условия подобия, будут отличаться друг от друга.
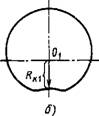
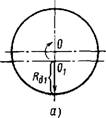
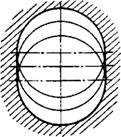
Изложенное можно проиллюстрировать на следующем примере. Возьмем профиль, имеющий в сечении окружность (рис. 1.6.46). Если построить круглограмму из центра, совпадающего с центром окружности, то отношение Яд,/Яд, = const, отсюда и AR,= const, поэтому на круг - лограмме будет тоже окружность (рис. 1.6.46, а).
При смешении центров (Яд,/Яд1 ф const), приняв за Ra] наименьший радиус Лд, = R0 - е, где R0 - радиус окружности детали; е - эксцентриситет, получим, что Яд,/Яд, будет изменяться при изменении направления луча, что приведет к нарушению условия подобия, и профиль круглограммы будет отличаться от окружности (рис. 1.6.46, б).
|
|
Такие измерения были приведены на кругломере мод. 218 Московского инструментального завода "Калибр". На измерительный стол установили сферу-эталон. Сначала произвели центрирование ее относительно измерительного шпинделя с высокой точностью (стрелка, указывающая точность центрирования, была практически неподвижна), затем была произведена запись круглограммы, которая почти не отличалась от окружности; эталон сдвинули и опять сцентрировали, но с низкой точностью (стрелка колебалась в пределах шкалы центрирования), опять записали круглограмму, которая уже значительно отличалась от окружности и была близка по форме к круглограмме, изображенной на рис. 1.6.46, 6.
|
|
Рис. 1.6.46. Круглограммы окружности:
А - при совпадении центров окружности и круглограммы; б - при несовпадении центров окружности и круглограммы
Аналогичные результаты были получены и при измерении на кругломере "Talyrond" (Великобритания) (в обоих случаях на круглограммах получили фигуру типа улитки Паскаля).
Таким образом, при отображении профиля с помощью круглограммы, построенной по отклонениям модуля радиус-вектора, надо помнить, что форма профиля детали может отличаться от формы профиля, записанного на круглограмме. На практике такое явление называют масштабным эффектом.
Отображение формы детали в виде развертки осуществляется следующим образом. При вращении детали с постоянной угловой скоростью измерительное устройство измеряет радиус детали относительно выбранного центра отсчета (обычно он совпадает с центром вращения) и через соответствующий механизм наносит на бумаге, движущейся поступательно со скоростью v, линию изменения радиуса в определенном масштабе. При этом должно соблюдаться постоянство отношения со / v. В зависимости от изменения отношения co/v запись кривой будет растянута или сжата. В общем случае зависимость радиуса от угла поворота в прямоугольных координатах:
Лр = К«[Лд„т + ДЛд(ф)], (1.6.12)
Где /?р - ордината развертки; /?дтіп - минимальный радиус детали относительно выбранного центра отсчета; АЛд(ф) - отклонение радиуса детали от минимального значения в функции угла поворота.
Из (1.6.11) следует, что при изменении масштабного коэффициента будет изменяться радиус развертки не только из-за колебания радиуса детали, но и из-за /?дтіП, т. е. график Rp -/(ф) не только изменится по ам плитуде, но и сместится по оси ординат. Условие подобия при таком спо собе отображения формы детали не нарушается, поскольку каждое зна чение радиуса Rai для соответствующего угла ф, умножается на один и тот же коэффициент Км, а площадь, необходимая для ее отображения, при значительном увеличении сравнительно невелика.
Аналогичным образом фиксируют результаты измерения профиля и в поперечных сечениях опорных шеек, относительно которых задано по ложение контролируемого сечения. В итоге получили исходную инфор мацию, необходимую для оценки геометрических погрешностей детали, т. е. для определения погрешности детали.
Рекомендуют измерять погрешности геометрических характеристик в следующей последовательности: погрешность геометрической формы поверхностей (микроотклонения, волнистость, макроотклонения), погрешность относительных поворотов поверхностей; погрешность размера или расстояния.
В рассматриваемом случае требуется определить отклонение от круглости профиля поперечного сечения вала, отклонение его положения относительно опорных шеек и отклонение диаметрального размера.
Этап 3 - измерение отклонения от круглости профиля поперечного сечения вала. Чтобы измерить отклонение от круглости, надо прежде всего определить базу отсчета. В качестве базы отсчета принимается геометрический прототип, заданный конструктором; в рассматриваемом случае это будет окружность.
При построении базовой окружности требуется найти положение ее центра относительно измеренного профиля. Поскольку реальный профиль имеет вид замкнутой кривой произвольной формы, то отклонение от круглости будет зависеть от положения центра базовой окружности. В соответствии с этим очень важное значение приобретает разработка правил определения положения центра базовой окружности и ее диаметра.
Наибольшее распространение нашли три методики построения базы отсчета отклонения от круглости профиля. ГОСТ 24642-81 предлагает в качестве базы отсчета отклонения от круглости пользоваться прилегающей окружностью. При этом под прилегающей окружностью понимается окружность минимального диаметра, описанная вокруг реального профиля наружной поверхности вращения, или максимального диаметра, вписанная в реальный профиль внутренней поверхности вращения.
В стандартах других стран в качестве базы отсчета принимается или средняя окружность, или две концентричные окружности. Средняя окружность проводится таким образом, чтобы сумма квадратов расстояний от нее до точек профиля, измеренных по достаточно большому числу равномерно расположенных и радиально направленных отрезков, являлась минимальной.
При отсчете погрешности формы от прилегающей и средней окружностей принимается максимальное отклонение точек профиля от окружности в радиальном направлении. Когда оценка отклонения от круглости производится с помощью двух концентричных окружностей, они проводятся так, чтобы одна из них была вписанной, а другая - описанной, при
чем принимается за базу такая пара окружностей (в общем случае может быть несколько пар концентричных окружностей), у которой расстояние в радиальном направлении между окружностями минимально.
Определение отклонения от круглости по этим трем методикам у одной и той же детали дает разный результат.
Главным недостатком рассмотренных выше методик отсчета погрешности формы является их использование независимо от служебного назначения контролируемой детали. Между тем детали одной и той ж»; заданной формы могут быть предназначены для выполнения различных служебных функций. Например, вал может выполнять роль плунжера, шпинделя или неподвижной оси. Отсюда следует, что методика отсчета погрешностей формы должна выбираться с учетом служебного назначения детали. Причем речь идет не только о правилах построения базовой окружности, но и о выборе критерия оценки погрешности. Если, к примеру, профиль опорной шейки можно оценить по максимальному отклонению точек профиля от окружности, то для плунжера нужна оценка гю площади отклонения, так как от ее величины зависит объем утечки рабочей среды.
В связи с этим представляет большой теоретический и практический интерес разработка методик определения погрешностей формы в зависимости от служебного назначения контролируемой детали.
|
Рис. 1.6.47. Профиль поперечного сечения детали с несколькими прилегающими вписанными окружностями максимального диаметра |
Недостатком методики отсчета погрешности формы от прилегающей окружности является неоднозначность решения. Если воспользоваться правилом определения прилегающей окружности, линии, плоскости, приведенные в ГОСТ 24692-81. то можно получить неоднозначный ответ, когда относительно одного и того же профиля поверхности детали может быть по строено несколько прилегающих окружно стей, линий, плоскостей. В качестве приме ра на рис. 1.6.47 показана фигура, в которую можно вписать множество прилегающих окружностей одного и того же максимшп. ного диаметра.
После определения базы отсчета производится определение отклонения от круглости, которое осуществляется непосредственным ее измерением или расчетом.
Например, измерение отклонения от круглости от прилегающей окружности осуществляется следующим образом. После записи круглограммы на последнюю накладывают прозрачный шаблон с нанесенными концентрическими окружностями, находят прилегающую окружность и определяют максимальное отклонение точки профиля круглограммы от прилегающей окружности; затем для определения погрешностей формы найденную величину делят на масштабный коэффициент. В других случаях к кругломерам прилагаются специальные вычислительные приставки, которые по результатам измерения рассчитывают погрешность формы.
После измерения погрешности формы переходят к измерению погрешности диаметрального размера профиля поперечного сечения вала.
Этап 4 - определение отклонения диаметрального размера поперечного сечения вала. Традиционно диаметральный размер измеряют как расстояние между двумя параллельными прямыми. Поворачивая деталь, производят несколько таких измерений и судят о их величинах по максимальному значению или принимают во внимание какое-то среднее значение от измеренных величин. Как видим, отсутствует; строгость в определении диаметрального размера, связь между служебным назначением детали и методикой определения диаметрального размера, связь между диаметром и формой профиля.
Этот вопрос практически не разработан, что существенно снижает точность измерения погрешности детали. Поэтому при определении по - ірешности диаметрального размера надо в первую очередь решить, что принимать за диаметр профиля произвольной формы; возможно, за диаметральный размер следует принимать диаметральный размер окружно - с ти, выступающей в качестве базы отсчета.
Следующим шагом должно быть измерение положения контролируемого профиля поперечного сечения.
Этап 5 - определение положения профиля поперечного сечения относительно опорных шеек вала.
Если подходить к решению этой задачи строго, то следует сформу - нировать критерии оценки погрешности относительного положения Профиля произвольной формы, выбрать базу отсчета, определить правила ее положения аналогично тому, как определяется погрешность формы поперечного сечения.
Если в качестве базы отсчета принять ось вращения, то надо определить центры вращения опорных шеек, провести через них ось вращения и относительно нее определять отклонение положения конструируемого профиля поперечного сечения вала.
На практике контроль относительного положения профиля часто осуществляется посредством измерения радиального биения. С этой целью деталь устанавливают опорными шейками в измерительном приборе и по схеме измерения радиус-вектора определяют радиальное биение как разность А наибольшего и наименьшего расстояний от точек реального профиля поверхности вращения до базовой оси в сечении плоскостью, перпендикулярной базовой оси.
Поскольку в качестве базовой оси используют оси опорных шеек, имеющих в свою очередь погрешность формы, постольку появится дополнительная погрешность измерения, обусловленная неточностью вращения.
Из приведенного примера можно сделать следующие выводы.
1. К основным причинам, снижающим качество и эффективность процесса измерения точности машины и деталей, относятся:
- многоступенчатость процесса измерения, приводящая к существенному накоплению погрешностей измерения;
- многочисленность и разнообразие геометрических характеристик, требующих контроля;
- отсутствие строгих связей между отклонениями геометрических характеристик;
- отсутствие связей между методиками их определения со служебным назначением контролируемого объекта.
2. Устранение указанных недостатков должно вестись в направлении математического описания процесса измерения, который сведется только к измерению поверхностей контролируемого объекта, унификации геометрических характеристик, что значительно снизит объем измерений и существенно уменьшит разнообразие методов и средств измерения, а также в установлении функциональных связей между отклонениями геометрических характеристик и служебным назначением изделия, установлении связей между геометрическими характеристиками контро лируемого объекта.