Оптоэлектроника

Насыщение в лазерных усилителях

В главе 3, а потом вновь в главе 4 мы видели, каким образом оптическое усиление, возникающее из стимулированной эмиссии, быстро насыщается. Это насыщение описывалось (4.10), и выражение для него вновь будет выведено в этом разделе. Рассмотрим четырехуровневую систему (рис. 4.3), в которой носители в основном состоянии |0) переводятся оптической накачкой (Я) в возбужденное состояние |3). Предполагается, что носители с уровня |3) мгновенно релаксируют на уровень |2), который, в свою очередь, характеризуется большим временем жизни. После чего начинает развиваться процесс стимулированного излучения, включающий излуча - тельную релаксацию носителей с уровня |2) на уровень |1) с характеристическим временем тг И, наконец, предполагается, что последующий процесс релаксации между уровнями |1) и |0) протекает мгновенно. Эта ситуация описывается следую­щей системой дифференциальных уравнений:

D^2 D N 2

—- = R - <т„„ЛГ, Ф------ г-

(4.Б.1)

Где Ф — фотонный поток, а сгр — оптическое поперечное сечение для перехода |2) -> |1). Стационарная плотность электронов ТУ2 на уровне |2) в этом случае дается соотношением:

Ы2 =--------- ^^----------------------------------- (4.Б.2)

2 1 + Ф/Ф,* 1 + Ф/Фза,

Где А^0 — малосигнальная плотность инверсной заселенности, а Ф5а1 — поток насыщения /<уо тг Усиление усиливающей среды в этом случае определяется

У = а^Ы2 ~ #,)°Рили:

ГшъЬй (4'Б'3)

Где у0 = сгорЯт2 является усилением холодного резонатора для среды, а интенсив­ность насыщения определяется соотношением:

Напомним, что, как правило, эта величина достаточно мала. Например, при попе­речном оптическом сечении 4 х 10-19 см-2, времени жизни 1,2 мс и энергии перехода Н (о = 1,16 эВ, /м1 ~ 500 Вт/см2, что соответствует достаточно малой плотности опти­ческой мощности.

Рассмотрим теперь область лазерной среды длиной Ь и площадью поверхности >4, которую мы используем в качестве усилителя. С одной стороны мы введем све­товой пучок с интенсивностью / и будем искать интенсивность пучка / на выходе каскада усиления. В этом усилителе отсутствуют зеркала, которые могли бы обес­печить оптическую обратную связь. Напомним, что если усиление в среде распро­странения составляет у то напряженность электрического поля пропорциональна е^2, а его интенсивность е*. Поскольку усиление обладает зависимостью от интен­сивности вследствие эффектов насыщения (уравнение (4.3.Б)) и поскольку интен­сивность есть функция координаты ъ интенсивность света в среде является, таким образом, решением дифференциального уравнения:

(4.Б.5)

Это уравнение может быть легко проинтегрировано с тем, чтобы получить зависи­мость интенсивности / от координаты I в среде в виде выражения:

(4.Б.6)

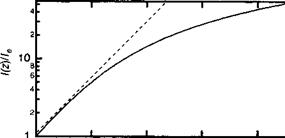
На рисунке 4. Б. 1 представлено изменение интенсивности в функции координаты ь Заметим, что по мере того, как интенсивность возрастает, в функции коорди­наты, наряду с усилением, наблюдается насыщение среды. Принимая <7 в качестве полного усиления усилителя, а (<7 =///) как малосигнальное усиление (<70 = е^), можем переписать уравнение (4.Б.6) в виде:

(4.Б.7)

Из этого последнего уравнения видно, что <7 быстро стремится к 1, когда ин­тенсивность света превышает его пороговую величину в среде. Приведенный ниже пример проиллюстрирует изменение усиления <7 лазерной среды с малосигналь­ным усилением 800. Заметим, что доступная величина усиления быстро уменьша­ется с /. Так при плотности мощности оптического излучения на входе 882 Вт/см2 усиление составляет всего 4, а выходная плотность мощности равна 3530 Вт/см2. Таким образом, насыщение является негативным и неустранимым эффектом, как это сейчас мы постараемся объяснить.

Обозначим через оптическую мощность, потребляемую усиливающей средой, т. е. 1&Р = ^ ~ /.■ В этом случае выражение (4.Б.7) дает:

Если пренебречь логарифмическим членом перед линейным членом в (4. Б.6), то в этом случае (4.Б.6) может быть записано в виде:

= (4.Б.8Й)

Или, вновь используя другой набор параметров, получаем:

_ М,0П СО

Максимально достижимая мощность излучения оптического усилителя, ограниченная оптическим насыщением

Это последнее уравнение устанавливает тот факт, что максимальная мощность, которую способен передать усилитель падающему световому пучку, дается энерги­ей й со, запасенной каждым атомом в состоянии инверсной заселенности (с плот­ностью Л^0) в течение времени т2.

Пример -------------------------------------------------------------------------------------------------------------

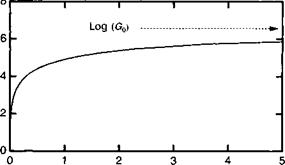
При использовании в качестве усиливающей среды Ы&УАв с уровнем легирова­ния 1019 см-3 максимальная плотность накопленной энергии в этом случае дается 1019 см-3 х 1,16 х 1,6 х 10-19 Дж или 1,85 Дж см-3. Максимальная плотность мощ­ности, которая может быть передана падающему пучку составляет в этом случае 1,85 Дж см_3/1,2 мс или 1,54 кВт см 3. В случае усилительного каскада длиной в 1 м мы получаем таким образом максимальную плотность мощности в 154 кВт см-2. Малосиг­нальное усиление составляет у0 = сгор = 4 х 10-19 см2х 1019 см3 = 4 см-1. Усиление усилителя в функции уровней входной и выходной мощности, определяемой (4.Б.7) (при (?0 = 2 х 1 м х 4 см"1 = 800), иллюстрируется рис. 4.Б.2.

Другим аспектом насыщения усиления в лазерных усилителях является искаже­ние формы импульса. Естественно, поскольку амплитуда импульса нелинейно влияет на коэффициент усиления, различные части оптических импульсов будут подверже­ны различному уровню усиления, что приводит к сильным искажениям импульса. Этот эффект имеет большое значение в оптических волоконных усилителях и очень важен для широкой гаммы практических применений в телекоммуникационных тех­нологиях — сейчас мы обсудим это.

Рассмотрим оптический импульс потока Ф1п(0> входящего в волоконный усили­тель. Заселенность усилителя инвертирована до момента отсчета Г = 0 так, что скорость накачки Я равна нулю во время усиления импульса в волокне. Более того,

Мы пренебрегаем спонтанной эмиссией (слишком медленной) в течение длительно­сти импульса. Теперь обратим наше внимание на отрезок волокна между х и х + д* в течение временного интервала между / и / + <1/. Уменьшение скорости заселенно­сти #2(х, Г) за счет стимулированной эмиссии под воздействием фотонного потока Ф(х, /) дается (4.Б.1), т. е. с учетом приведенных выше допущений:

^М2(х, /)= - сгорЛ/2(х, /)

Пространственно-временная эволюция фотонного потока описывается уравне­нием непрерывности. Сейчас мы повторно выведем его, поскольку это всегда очень стимулирующее упражнение! В интервале Ах поверхностная плотность фотонов /?рЬ связана с фотонным потоком соотношением Ф(х, /) = с'р(х, /), где с? — скорость света в волокне. Скорость изменения числа фотонов в интервале Ах дается суммой потока фотонов на входе и скорости стимулированной эмиссии в интервале Ах за вычетом фотонного потока на выходе, т. е.:

Что приводит к уравнению непрерывности:

-^Ф(х, /)+ С'-^ф(х, г)= °^2(х, Ф(х, /)

^■ЛГ2(м)= -<г0рЫ2{х, /)ф(х, /)

Уравнения распространения импульса в лазерном усилителе

Выше мы повторно записали уравнение (4.Б.10), поскольку все, что нам необ­ходимо сделать для решения вопроса об искажении формы импульса из-за насы­щения в усиливающих волокнах, так это решить два последние связанные нели­нейные уравнения.

Подобно всем уравнениям распространения (4.Б.11) могут быть решены в систе­ме эйлеровых координат. Это означает, что мы должны следовать за распространени­ем импульса «верхом» на фотонах, иначе говоря, вводя новую систему координат:

/ = / х = х + СІ

По определению плотность фотонов и инверсная заселенность в этих новых координатах представляют собой:

(4.Б.12 б)

И2(х, і) = N2(x, О

Величина Ф (константа, /) «разделяет судьбу» импульса в процессе его распрост­ранения в волокне. Якобиан трансформации системы координат может быть предо­ставлен в виде:

(4.Б.12в)

Э _ Э дх ^ Э Э/

Э/ дх дх Э/ х

Таким образом, новая система координат (4.Б.10) и (4.Б.11) принимает вид:

^-ф(3с, Г)= AofN2(x, ф(3с, /) Дг-іуДх, 7)= -o-opyv2(?, Г)і(х, 7)

Распространение импульса в лазерном усилителе в движу­щейся системе координат

Уравнения (4.Б. 13) и (4.Б. 14) выглядят симпатичнее, чем аналогичные уравне­ния в системе координат Лагранжа. В действительности же это обман зрения: все сложности теперь переносятся на граничные условия, которые теперь становятся комплексными, но в оставшейся части распространения мы пренебрежем этим ас­пектом. Дадим им теперь интегральную формулировку (4.Б.13) и (4.Б.14), что в действительности известно как модель Франца—Нордвика. С этой целью мы интег­рируем (4.Б. 13) по длине волокна с маленькой хитростью использования гранич­ных условий при х = 0 и х = Ь (оставляя читателю задачу определения критериев справедливости этих граничных условий):

J тУнП^= Сор J^2^’ » <7opWr(/) (4.Б.15)

Ф (f) ' ’ ' х = О

Где, по определению, А^/) есть интегральная инверсная заселенность по длине волокна (см-2). Из (4.Б. 15) сразу получаем:

(4.Б.16)

Где G(t) — мгновенное усиление лазерного усилителя. Теперь (4.Б.13) и (4.Б14) можно «слить» с тем, чтобы получить второе интегральное уравнение:

Так, что:

(4.Б.176)

Последнее уравнение утверждает, что усиление потока в волоконном усилителе равно уменьшению интегральной инверсной заселенности, что само по себе имеет смысл. Теперь мы можем решить систему, образованную (4.Б.16) и (4.Б.17б) с тем, чтобы в первую очередь описать временную эволюцию интегральной инверсной заселенности:

(4.Б.18)

Вводя фотонный флюенс как временной интеграл фотонного потока:

(4.Б.19)

Мы получаем уравнения для описания временной эволюции интегральной инверс­ной заселенности, мгновенного усиления и выходного фотонного потока:

С0-(е0-1)е

Фо„,(0=Ф»(/)

Уравнения Франца—Нордвика

Где есть флюенс насыщения, (70 — ненасыщенное усиление усилителя ((70 = <торЛ^0)

И - начальная интегральная инверсная заселенность или полный флюенс в

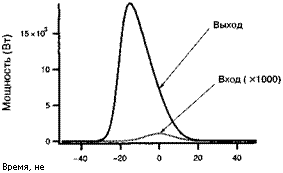Волокне (см-2). Эти три уравнения описывают искажение формы импульса в лазер­ном усилителе. Например, если на входе в волокно вводится импульс прямоуголь­ной формы Фт(/) = Фт, то, как показывает уравнение (4.Б.22), выходной импульс будет затянут с экспоненциальной постоянной времени е-^0-1. В другом случае (гауссовский импульс на входе) анализируется в качестве примера, который приво­дится ниже, а результаты этого анализа иллюстрируются рис. 4.Б. З. На представ­ленном рисунке явно видно проявление эффекта искажения формы импульса.

Рис. 4.Б. З. Искажение формы им­пульса в волоконном усилителе из - за насыщения (смотрите пример).

Наконец, как в случае непрерывного (С¥) режима, рассмотренного в начале этого раздела, легко определить максимально достижимую энергию £ , которую можно извлечь из волоконного усилителя:

£сър = НТ0На> (4.Б.23)

Этот расчет мы оставляем читателю в качестве упражнения.

Пример ---------------------------------------------------------------------------------------------------------------------------------------------------

Исследуем поведение волокна, легированного эрбием, длиной 2 м с внутренним диаметром 8 мкм и уровнем легирования 7 х 1019 см-3. Длина волны излучаемых фотонов составляет 1,55 мкм (0,8 эВ), а оптическое поперечное сечение Ег3+ в кварцевом волокне принимается равным 10-21 см-2. В этом случае флюенс насыще­ния составляет:

= 1/(10-21 см-2) = 1021 см-2.

Полный флюенс Л^0, который можно извлечь из волокна, в соответствии с (4. Б. 15) составляет:

Nто — 7 х 1019 см-3 х 2 х 102 см = 1,4 х 1022 см-2

Т. е. он в 14 раз превышает флюенс насыщения. Таким образом, следует ожидать сильного искажения импульса. Полная энергия, извлекаемая из волокна (4.Б.23) составляет:

= 1,4 х 1022 см-2 х 1,6 х 10-19 Дж х 0,8 эВ [3,14 х (8 х 10"4)2 см2/4] = 0,9 мДж

Приведенная ниже программа MATEMATICA дает пример искажения гауссов­ского импульса.

1 9А

N0 = 7.1019 (*ст-3*); (сг=1.10 21 (*ст-2*); hv = — 1.61СГ19;

1.55

Usвt = — (*J/cm2‘); Dfibre = 810'4(* 8ju т *) S = n|* Dfibre2/а] г = 10(* ns *)

О

(fibre = 200(* 2m *) GO = Exp[<r NOIfibre] IO = -(* IWinput *)

(* W/cm 2 *) Uin = 10'9I0Jexp

#[t_]: —— f lin[t]dt; Nrel =--------------------------- Log

L J Usвt J a NOIfibre y

GO

GO - (GO - 1)Ехр[- <9(t)J

; Lout = S———. ^9—і—7Tilin[t}

GO - (GO - l)Expl - в (t)J li

P1 = Plot[linp, {1,-50,50}

PlotRange-» All, PlotStyle -» RGBColorf), 0, о] DisplayFuction -» Identity]; p2 = Plot[lout,{t,-50,50}

PlotRange-> All, PlotStyle -»RGBColor{0,1,0] DisplayFuction -»Identity]; Show[p1, p2, DisplayFunction -» $ Display Function, AxesLabel -»

-» {"t(ns)','Pout(W)'}]