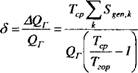Термодинамическая оптимизация
|
А) |
В последние 10 лет в мире появились многочисленные публикации в области термодинамического анализа сорбционных машин как частного случая теплоиспользующих холодильных машин и тепловых насосов. В этих публикациях уточняются существующие и предлагаются новые подходы к термодинамическому анализу цикла
машин с целью определения оптимального или рационального режима работы. Это, по мнению многих исследователей, позволит существенно уменьшить размерность задачи оптимизации с использованием экономических критериев, например, методами термоэкономики, так как в термоэкономической оптимизации предполагается рассматривать только те варианты, которые являются приближенными к оптимальным с точки зрения термодинамической оптимизации. Таким образом первоначально рассмотрению подлежит идеальный цикл анализируемой теплоиспользующей машины.
Поскольку идеальным циклом-образцом для всех теплоиспользующих машин (а также машин с приводом от теплового двигателя) принимают цикл Карно-Карно, то осуществим попытку термодинамической оптимизации этого цикла.
Для построения термодинамического цикла любой теплоиспользующей машины необходимо располагать тремя* источниками тепла различных температурных потенциалов (рис. 19.4):
• высокопотенциальным - Тгор
• среднепотенциальным - Тср;
• низкопотенциальным - Тхол.
Многие авторы без каких-либо оснований утверждают следующее: если три основных температурных уровня работы теплоиспользующей машины будут изменяться произвольно, то путем термодинамической оптимизации можно определить такой режим работы, в котором СОР-max.
Наиболее распространенным подходом является использование методов высшей математики по исследованию функции нескольких переменных СОР^ор = 1(Тгор, Тср, Тхол ) с целью определения экстремума. В этом случае ур.(19.2) получит вид
ДСОР™ор дСОР™ор
|
ДСОртеор |
|
|
|
DCOP™op = |
|
|
На этом этапе анализа необходимо доказать применимость инвариантности формы первого дифференциала к исследуемой функции: полный дифференциал функции сохраняет один и тот же вид независимо от того, являются ли ее аргументы независимыми
С точки зрения терминологии, принятой в термодинамике сорбционных систем, теоретический цикл иногда называют «циклом на трех температурных уровнях».
Переменными между собой или функциями от независимых переменных. Поскольку в качестве переменных функции СОР£еор выступают три температурных уровня источников тепла, то будем считать, что они изменяются непрерывно и вне зависимости друг от друга, при соблюдении одного условия Тхол< Тср< Тгор.
Любой метод математического моделирования, в основе которого лежит дифференциальное исчисление, может быть использован как основной математический аппарат в анализе и оптимизации только при условии, что функция оптимизации дифференцируема во всех точках. С точки зрения решаемой задачи это означает, что должно существовать хотя бы одно схемно-цикловое решение тепло - использующей машины для любого сочетания Тхол, Тср, Тгор (на этом этапе анализа вопрос термодинамической и/или экономической эффективности схемно-циклового решения машины роли не играет, главное условие - принципиальная работоспособность машины). Это условие полностью выполняется для абсорбционных холодильных машин и частично - для других типов теплоиспользующих машин, поэтому можно констатировать, что для всего класса теплоиспользующих холодильных машин функция СОРна уровне анализа цикла Карно-Карно дифференцируема во всех точках.
Поскольку анализировать цикл без схемы невозможно (на основании вышеописанных ограничений), то предположим существование схемного решения теплоиспользующей машины, состоящей из генератора, турбины, конденсатора и компрессора как элементов для осуществления прямого термодинамического цикла, а также испарителя, компрессора, конденсатора и детандера - для осуществления обратного цикла. Тепловой баланс такой машины описывается ур,(19.3). Для использования цикла Карно-Карно как цикла-образца, переформулируем условия проведения анализа:
• наличие трех источников тепла с постоянными температурами (Тгор-const; Тср-const; TXOJl-const);
• подвод и отвод теплоты к рабочему телу осуществляется при постоянных температурах[58] (Tr~const; TKj-const; T^-const; Ти=const);
• наличие идеального теплообмена АТк=0 (Тгор~Тг; Тср-ТК1;
• наличие идеальных процессов сжатия и расширения;
• вся работа, произведенная в прямом цикле, потребляется в обратном.
Исследование функции, выраженной ур.(19.3), по каждой из переменных (ур.(19.6)) является достаточно громоздким, поэтому рассмотрим конечный результат в виде дробно-рациональной функции, уравнение которой в общем виде записывается как
У= — —I—-------- где х переменная; А, В, С - коэффициенты.
Ах2 +Вх + С
Общий вид возможных графиков дробно-рациональной функции приведен на рис. 19.8. Видно, что случай у=О возможен только при Л>0, поэтому достаточно определить величину А для анализа (нет смысла приравнивать нулю частные производные функции СОР™еор
Если А<0, так функция СОР™еор экстремума не имеет). Результаты анализа таковы:
• влияние температуры греющего источника
Э СОРГор 1
---------- — = ——. (19.7)
Гор [59] гор
_ const „ _
Функция вида у-—— представляет частный случаи дрооно-
Рациональной функции. Если N - целое число, то функция монотонно возрастает и экстремума не имеет. Таким образом функция
СОР™еор (Тгор) экстремума не имеет;
• влияние температуры окружающей среды
*С£2£_=_________________________ I______________________ (19.8)
FT Т 9 Т Т
01 ср гор___ 1 гор rp | гор
Т (т - т ) ср Тт т 5 ср (т Т 1
Ход гор хол / у1 гор хол} угор хол /
Анализ показывает, что А=0, следовательно, функция СОР™еор (Тср) экстремума не имеет;
Рис. 19.8. К анализу дробно-рациональной функции
|
Т т ГОР 'гор |
|
|
Прямой |
|
|
У цикл |
|
|
Тср S Тхол |
|
|
Обратный |
|
|
Цикп s |
|
А) |
|
30 40 60 60 70 80 90 100 110 120 130 140 150 160 ТГ0| б) Рис. 19.9. К изучению функции СОР"еор: а) СОР*еор =<*>■, б) СОРТ0" = ЛТгор, Тср, Тхш ) |
|
(19.9) |
• влияние температуры производства холода дСОР™ор 1
Анализ показывает, что А=0, следовательно, функция СОР™еор (Тхол) экстремума не имеет.
Случай СОР£еор= оо соответствует Тгор = с» и Тср = Тхол, для которого цикл-образец Карно-Карно изобразится в виде соединения двух прямых (рис.19.9а): вертикальной, описывающей прямой цикл, и горизонтальной, описывающей обратный цикл. Результаты численного анализа, представленью на рис. 19.96 в виде семейства восходящих поверхностей, подтверждают теоретические исследования.
С точки зрения эксергетического анализа было принято условие £д*=0 для всех элементов. Для двух компрессоров это означает работу при изоэнтропном сжатии, детандера и турбины - при
Изоэнтропном расширении. Для четырех основных теплообменных аппаратов условие EDk=Q соответствует АТ^О, следовательно будет иметь место бесконечно большая теплообменная поверхность этих аппаратов Fk—и, как результат, бесконечно большая их стоимость Топливом (приводной энергией) для любой теплоиспользующей машины является тепло, подведенное к генератору. Продуктом холодильной машины является холод, произведенный в
|
СР |
( т„ ^
|
Т, Хоп у |
Испарителе, тогда эксергия продукта - EPI =EP0=Q0
1-
|
( т Л Ср Т Гор |
|
Efz — Ер г — Qr |
- эксергия топлива, затраченная в
Генераторе. Следовательно, при и Тср = Тхол, эксергетическая
Эффективность теплоиспользующей холодильной машины
Рассмотрим второй этап «метода циклов» для анализа теплоиспользующей холодильной машины - введение необратимости в процессы подвода-отвода тепла - с точки зрения определения экстремума функции СОРВ этом случае EDk ФО для тепло - обменных аппаратов, что будет соответствовать теплообменным аппаратам с конечными размерами теплообменной поверхности Fk и ограниченной стоимостью Z*.
Цикл с необратимостью в процессах подвода-отвода тепла приведен на рис. 19.10а. Условия проведения анализа:
• наличие трех источников тепла с постоянными температурами (Тгор~const; Tcp~const; Тхол - const)]
• подвод и отвод теплоты к рабочему телу осуществляется при постоянных температурах (Tr=const; Тк}-const; ТК2-const; TM~const)
• наличие реального теплообмена АТф) (ТГ-Тгор-АТГ; ТК1=ТК2 =Тср +АТ&; ТИ - Тхоя —ATи) ;
• наличие идеальных процессов сжатия и расширения;
• вся работа, произведенная в прямом цикле, потребляется в обратном.
Верхний индекс «ег» соответствует endo-reversible циклу, т. е. циклу только с необратимостью в процессах подвода-отвода тепла (п.5.1).
А) б) в) r)
Рис. 19.10. Анализ цикла Карно-Карно с необратимостью в процессах подвода-отвода тепла
В соответствии с условиями проведения анализа выражение для определение COPz имеет вид
|
Сор;г=сор," • сор: |
|
Обратный |
|
. (19.10) |
|
(Тгор-ЛТг)-(Тср+ЛТк]) |
|
— г°р |
|
(Тгор-АТГ) |
_ тг тк1 ТИ _ Тг ТК2 - ТИ (ТХШ-ЛТИ) (Т+АТ^ЫТ^-АТи)
|
Эквивалентен |
|
Гор |
Анализ выражения для определения
ДСОРег
Анализу по ур.(19.7), выражения------------- — - по ур.(19.8) и выражения
ДТ,
Ср
Д СОРІ
По ур.(19.9).
ДТхш
Проанализируем влияние величины АТк в теплообменных аппаратах. Поскольку ТК1=ТК2, то для упрощения анализа будем оперировать только величинами Тк и АТК, тогда
ЭАТГ (Тк + Ти) ДТ2 2Тгор(ТК + Ти) „ , {тк +ти)
-____________________ г ' _____________ ,----------- ,(19-12)
ДЛТ« Tr jT2, 2Тг{Тср-ТИ)лт i Тг{Тср-ТИУ
ТИ{тг-тИ) к тИ{тг-тИ) к тИ(тг-тИ)
Любой действительный процесс сопровождается необратимыми потерями, что описывается величиной производства энтропии Sgen, k (глава 2). Необратимости в процессах подвода-отвода тепла, введенные в цикл Карно-Карно (рис. 19.10а), должны быть отражены в тепловом балансе
Teop(ASr+Sgen, r ) + Txa(/ISll+SgmJI) =
(19.14)
= Tcp(ASK+Sgm, K).
Исходя из теории теплоиспользующих машин, величина Qr представляет теоретически необходимое, т. е. минимальное, тепло высокого потенциала - топливо. Величина AQr должна «компенсировать» все необратимости в машине при условии, что продукт - холодопроизводительность Qo - остается постоянным
(Qr +AQr) + Qo = Qm +A <2[60]2. (19.15)
Для теплоиспользующих машин последовательность преобразования соотношения Гюи-Стодолы была предложена в 1930-ых годах Ф. Бошняковичем
П п п
Пl ~ Г1к gen к gen k - TaopSgenF, (19.16)
К=1 к=] к=І
Графическая интерпретация которой представлена на рис. 19.106,в.
Рассмотрим каждый этап. Общая необратимость представляет сумму необратимостей в каждом элементе и, в соответствии с теоремой Гюи-Стодолы, приведена к температуре окружающей среды (эта величина представляет суммарную деструкцию эксергии). Если «перенести» суммарную необратимость на температурный уровень греющего источника (Тгор), то последнее равенство в ур. (19.15) будет соответствовать теплу, дополнительно подведенному к генератору (теоретическому или действительному), т. е.
AQr =----------------- . (19.17)
J CP
Т
Гор
Безразмерный вид определения величины AQr удобно использовать для проведения анализа при работе в различных температурных режимах
|
Рис.19. Юг демонстрирует термоэкономический вывод из выполненного термодинамического анализа. При сохранении постоянным значения Тгор, соблюдается равенство |
|
(19.18) |
|
|
(19.19)
С точки зрения термоэкономики, условие Тгор соответствует постоянной цене на минимально и дополнительно подведенное тепло к генератору. Величина AQr определяется изменением расхода греющего источника, что пропорционально увеличению общей стоимости топлива.
Абсолютно очевидно, что условие T20p-const; Tcp-const; Тхол-const невозможно осуществить на практике, и постоянные температуры источников тепла должны быть заменены на переменные. Рассмотрим частный случай, когда для прямого цикла T2op^const и Терфсоти но для обратного цикла Tcp-const и Txo/l=const. В этом случае процесс конденсации прямого цикла (К1) должен быть рассмотрен раздельно от процесса конденсации обратного цикла (К2). Тогда ТгФ-const, TKrtcohst и Tia-const, ТИ=const. Цикл Карно-Карно (теоретический и с необратимостью в процессах подвода-отвода тепла) должен быть заменен на цикл Лоренц-Карно (предложен Т. В.Морозюк в 2Q01 году) - рис. 19.11. Для анализа цикла Лоренц - Карно ур.(19.14) имеет вид
Г
Гор
Тгор( + ) + (ASH + Sgenf„ )
|
Ті |
|
Гор |
Ур.(19.15)-(19.18) сохраняют свою актуальность при введении в
Рассмотрение средних температур Т™ и Т™ (ур.(2.31)-(2.32), рис.2.4).
Выражение для определения величины AQr для цикла Лоренц-Карнр
Может быть записано как AQr=Sgen>rT™p, однако при T20p? sconst
Ур.(19.19) и соответствующая графическая интерпретация (рис.19.10г) требуют пересмотра.
В общем виде величина Sgenir будет интерпретироваться как проекция на ось s продолжения изобары 1-2 в соответствии с выражением
У max
Sga, r = J ■ (19-21)
Tmm [61] гор 1гор
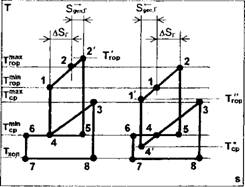
Аналогично анализу цикла Карно-Карно, величину Sgen>r можно графически добавить как справа, так и слева к процессу 1-2, при условии сохранения величины AQr постоянной (рис. 19.11):
• при расширении зоны генерации в область высоких температур (Sgen, r~*) - рис. 19.11а.
Тгортах = Т2< > Тъ Тгортш =Т,. Таким образом, при отнесении необратимых потерь к теплу более высокого температурного потенциала, увеличение эксплуатационных затрат теплоиспользующей машины связано с увеличением цены греющего источника;
• при расширении зоны генерации в область низких температур (S^/-)-рис. 19.116.
|
|
|
А) |
|
Рис.19.11. Основы термоэкономического анализа теплоиспользующей машины при рассмотрении цикла- б) образца Лоренц-Карно |