МАСЛОЭКСТРАКЦИОННОЕ ПРОИЗВОДСТВО

МЕХАНИЗМ ПРОЦЕССА ЭКСТРАКЦИИ

Поскольку процесс экстракции является процессом массо - обмена, то передача вещества в нем может происходить посред­ством молекулярной диффузии, конвективной диффузии, сочета­нием обоих видов диффузии и других видов массопередачи.

Молекулярная диффузия. К основным законам мас­сопередачи при молекулярной диффузии относятся первый и вто­рой законы Фика.

Первый закон говорит о количестве вещества, переносимого через элемент сечения. Представим себе, что перенос вещества от большей концентрации к меньшей идет по направлению стрелки.

Выделим в растворе объемный элемент длиной dx и пло­щадью поперечного сечения F. Предположим далее, что на гра­нице I концентрация растворенного вещества будет С, а осмоти­ческое давление1 р, на границе II соответственно — С—dC и р—dp на единицу поперечного сечения.

1 Осмотическое давление—это давление, которое оказывают молекулы' растворенного вещества внутри раствора.

Если диффузия происходит под влиянием разности осмоти­ческого давления, то это давление на границе I будет pF, а на границе II — (р—dp) F.

В этом случае движущая сила растворенной частицы будет

PF — (p — dp)F=dpF.

Так как скорость движения частицы пропорциональна силе; то можно написать, что количество вещества dm, проходящее за время dx через сечение F, будет

Dm =KdpF,

Dx

Где К — фактор пропорциональности.

Но количество вещества, переносимое через сечение F, обрат­но пропорционально длине выделенного элемента, следовательно

= (і) dx

Если осмотическое давление по закону Вант-Гоффа p = RTC,

Где: R— газовая постоянная;

Т — абсолютная температура; С — концентрация, т. е. число молей в 1 л, то при постоянной температуре dp=RTdC. Подставляя это вы­ражение в формулу (1), получим

, ьгтл'г dCd t F dm — KRT-

Dx

Обозначим постоянные величины KRT через D. Так как dm,

F и d*—величины ^положительные, а величина отрицатель-

Dx

-ная (концентрация убывает), то, ставя перед этим выражением знак минус, получаем выражение для первого закона Фика

Dm =~DF— dx. (2)

Dx

В этой формуле константа D есть количество вещества, ко­торое продиффундирует за время, равное единице, через сече­ние, равное единице, при разности концентраций, равной еди­нице.

Константа D называется коэффициентом диффузии, его раз­мерность — см2/сек. Если обозначим через q количество вещест­ва, переносимое в единицу времени через единицу поверхности, то первый закон Фика можно выразить так:

N dC

А =— D — . 7 dx

Таким образом, первый закон Фика выражает стационарный процесс диффузии и характеризует скорость переноса вещества

При постоянном градиенте концентрации ( —). При экстракции

1 dx і

Масличных семян практически имеет место нестационарный про­цесс диффузии, выражаемый вторым законом Фика, который говорит об изменении концентрации диффундирующего вещества в определенной точке в зависимости от времени. Он выводится из первого таким путем.

Если первое сечение (I) будет находиться от второго (II* на расстоянии dx, то в системе координат расстояние I от нача­ла их можно выразить через х, а расстояние II — через x + dx. Пусть время прохождения растворенной частицы от І до II бу­дет dx. В этом случае количество вещества в элементе dx будет равно разности прошедшего через х и через х-\-dx, т. е.

\ дх j дх

Деля ето выражение количества на объем, получим кон­центрацию

Д (dm)dx _ д (dm) dxFdx dxF

Но для изменения концентрации можно дать и такое вы­ражение

ДС,

flt.

Дх

Приравнивая ети два выражения друг другу, получим

Д (dm) дС,

TOC \o "1-3" \h \z г—- = а х,

ДхР д т '

Или

Д (dm) дС, -

і—> — d-zF.

Дх дх

Но из первого закона имеем, что

/ rfC \

Д I —О dxF\

\ dx )

Д (dm) \ dx /' ГЛ J г

— = = L) от г,

Дх dx дх2

TOC \o "1-3" \h \z дС, с - п й'С, с d^F = D dxF,

Дх дх2

ДС — £) д*С

Дх дх2

При молекулярной диффузии перенос вещества обусловли­вается тепловым движением молекул экстрагируемого вещества.

Применительно к жидкостям наиболее современной являет­ся «дырчатая» теория молекулярной диффузии [89].

С. точки зрения этой теории молекулярная диффузия зави­сит от размера молекул экстрагируемого вещества и от вязко­сти среды. Вследствие этого для данного вещества с увеличе­нием температуры возрастает и скорость молекулярной диффу­зии.

Зависимость молекулярного коэффициента диффузии от ука­занных выше факторов хорошо описывается формулой Эйн­штейна:

N6ni\r

Где: R — газовая постоянная; N — число Авогадро; Т — абсолютная температура; т| — абсолютная вязкость растворителя; г— радиус молекул диффундирующего вещества.

Эта формула, как указывает Френкель [90], хорошо согла­суется с данными опыта в тех случаях, когда размеры молекул диффундирующего вещества намного превышают размеры мо­лекул растворителя.

Конвективная диффузия. Перенос вещества в силу перемеще­ния одной фазы относительно другой как целого носит назва­ние конвекции.

Если причиной замещения фаз является разность концент­раций, то такой вид конвекции называется свободной, или естест­венной. Если перемещение вызвано внешними силами, то перенос носит название вынужденной конвекции. Для этого случая пе­реноса вещества зависимость между диффузионным потоком и разностью концентраций будет такова [91]

Q = - р (С, — С2), или q =- ЗА С,

Где: р — конвективный коэффициент диффузии (или константа скорости), который выражает количество вещества, переносимое через единицу поверхности в единицу вре­мени при разности концентраций, равной единице; его размерность—см2/сек;

А С — разность концентраций.

При конвективной диффузии в отличие от молекулярной влияние размера молекул, вязкости растворителя и других факторов незначительно и решающим для скорости переноса вещества будут скорость и режим движения жидкости, вяз­кость жидкости, характер поверхности и т. п.

Для процессов, в которых перенос вещества происходит как в силу молекулярной, так и конвективной диффузии уравнения массопередачи Фика должны дополниться конвективным чле­ном и будут таковы:

Для первого закона Фика

+ VXC;

Dx

Для второго закона

Дх dx2 дх '

Где Vx — составляющая скорости конвективного переноса ве­щества в направлении х.

Исходя из представлений о внутренней структуре экстраги­руемого материала и о распределении в нем масла, а также учитывая силы, которыми удерживается масло на поверхности частиц и в их порах (капиллярах), можно на основе суммиро­вания соображений различных исследователей {41, 64, 90, 91, 92, 93, 94, 95, 96] по вопросу механизма экстракции процесс извле­чения масла применительно к одной элементарной частице пред­ставить следующим образом:

А) смачивание растворителем экстрагируемой частицы и рас­творение масла, находящегося на поверхности частицы в сво­бодном состоянии;

Б) проникновение растворителя в толщу экстрагируемой ча­стицы, смыкание внешних и внутренних растворов в единую систему; . 1 1 Щ

В) движение масла вместе с потоком мисцеллы изнутри ча­стицы к ее поверхности по свободным поверхностям, по капил­лярам, через перепонки, создаваемые вторичными структурами, и через неразрушенные клеточные стенки масличного семени;

Г) диффузия масла, вышедшего с мисцеллой на поверхность частицы, через диффузионный слой, окружающий ее;

Д) конвективный перенос масла от внешней . поверхности диффузионного слоя в общий поток мисцеллы, движущийся в экстракционном аппарате.

Если, как было указано, рассматривать процесс экстракций применительно к изолированной элементарной частице экстра­гируемого материала, то перечисленные выше ступени переме­щения веществ будут во времени проходить последовательно. Однако, поскольку в практике обрабатывают материалы, обла­дающие значительной массой, указанная последовательность может не сохраниться, так как не успеет растворитель проник­нуть в частицу мятки или жмыха, как начнется растворение масла, движение. его к поверхности и т. п. Таким образом, пра­вильнее будет говорить о смещении этапов процесса экстракции во времени, т. е. проникновение растворителя начнется раньше, чем растворение масла, а растворение раньше, чем движение мисцеллы к поверхности частицы, а этот последний процесс начнется раньше, чем конвективная диффузия.

Рассмотрим 'процесс экстракции по намеченной нами схеме и отметим закономерности, определяющие отдельные ее фазы.

Смачивание экстрагируемых частиц растворителем и проник­новение его внутрь происходит:

Под действием капиллярных сил, развивающихся до тех пор, пока поры экстрагируемой частицы не заполнятся мисцел - лой (жидкостью); капиллярные силы помогают гидрофобному растворителю проникать в частицы, если стенки пор сухи и хо­рошо смачиваются; если стенки частицы материала в силу вы­сокой влажности не смачиваются, то капиллярные силы направ­лены в обратную сторону и мешают проникновению раствори­теля внутрь частицы;

В силу разности давлений внутри пор частиц и вне их; давление вне экстрагируемых частиц может быть как гидроста­тическим, так и гидродинамическим вследствие скоростного на­пора, создаваемого насосом;

Под действием сил диффузии паров растворителя, диффун­дирующих в воздух, находящийся в порах частиц экстрагируе­мого материала;

Под действием электрических сил (кинетического потен­циала), возникающих при движении растворителя в порах (капиллярах) частиц;

Вследствие адсорбции растворителя экстрагируемым мате­риалом.

Для установления факторов, влияющих на величину дви­жущих сил, рассмотрим законы, действующие на величины сил, ее слагающих.

Как известно, величина капиллярных сил определяется вы­сотой подъема жидкости в капилляры и может быть вычислена по формуле:

, 2 и cos в h =

Rg (Pi - Р2)

Где: h — высота подъема; г — радиус капилляря; g — ускорение силы тяжести; Єї — плотность жидкости; q2 — плотность окружающего воздуха; в — краевой угол смачивания; а — коэффициент поверхностного натяжения.

Как следует из формулы, высота подъема (всасывания) пря­мо пропорциональна коэффициенту поверхностного натяжения растворителя и обратно пропорциональна его плотности и ра - дтсусу капилляра. Таким образом, капиллярные силы зависят от природы растворителя, температуры его и структуры экстраги­руемого материала (лепестка, крупки). Чем 'пористей материал, тем больше капилляров в единице объема экстрагируемого ма­териала.

Величина разности давлений вне экстрагируемых частиц и внутри них зависит как от давления, создаваемого скоростным напором растворителя, т. е. от режима прокачки, так и от дав­ления в порах частиц. В свою очередь внутреннее давление в порах зависит от степени насыщения капилляров парами раство­рителя и от упругости паров растворителя над мисцеллой, т. е. от концентрации мисцеллы и от температурного режима экст­ракции.

В процессе проникновения растворителя внутрь экстрагируе­мых частиц гидростатическое давление внутри них будет расти и разность при соблюдении постоянства режима экстракционно­го процесса будет падать и в определенный момент уравняется, причем она перестанет действовать на проникновение раствори­теля в частицы позднее, чем" капиллярные силы.

Процесс экстракции связан со свободной диффузией раство­рителя в лоры и капилляры экстрагируемого материала. Дви­жущей силой в этом случае является, как известно, градиент концентрации, величина которого зависит от разности упруго­сти паров чистого растворителя внутри пор частицы и вне ее; упругость паров в свою очередь зависит от температуры и кон­центрации мисцеллы в различных участках экстрагируемого ма­териала. Так как концентрация мисцеллы в порах частицы выше, чем вне ее, то упругость паров растворителя внутри ее будет меньше, чем вне ее. Однако в дальнейшем по мере проникнове­ния растворителя в экстрагируемый материал и образования мисцеллы упругость его паров внутри частиц будет возрастать и диффузия растворителя в поры частицы постепенно будет затухать, а затем при выравнивании концентраций мисцеллы внутри и вне частицы совсем прекратится. Помимо этого, диф­фузия паров растворителя в капилляры прекратится при запол­нении капилляров жидкостью.

Электрические силы, возникающие от трения растворителя о стенки пор частицы экстрагируемого материала и влияющие на продвижение растворителя по капиллярам, зависят как от ско­рости проникновения, так и от особенностей структуры экстра­гируемого материала. Очевидно, что эти силы будут действо­вать все время, пока будет происходить прокачка растворителя.

Из сказанного следует, что общая движущая сила, побуж­дающая растворитель проникать внутрь частицы экстрагируе­мого материала, зависит от его масличности, структуры, при­роды растворителя, а также от температуры и давления, при которых ведется экстракция. Степень влияния этих факторов на величину движущей силы при смачивании и пропитке частицы экстрагируемого материала. различна, непостоянна, а некоторые факторы к тому же имеют только временный характер. Поэтому движущая сила смачивания и проникновения растворителя в ма­териал непостоянна и к концу процесса смачивания умень­шается.

Хорошо известно отрицательное действие на эффект экстрак­ции повышенной влажности экстрагируемого материала. Влага не только замедляет процесс смачивания частиц, «о иногда и вовсе блокирует от растворителя некоторые участки.

Можно считать, что в начале процесса экстракции рас­творитель будет проникать в экстрагируемый материал преиму­щественно в виде паров. Так как над слабыми мисцеллами уп­ругость паров растворителя выше, чем над концентрированными, то пары растворителя при слабых мисцеллах должны проникать внутрь экстрагируемого материала скорее, чем в случае крепких мисцелл.

Поскольку проникновение растворителя в экстрагируемый материал идет по капиллярам, то оно подчиняется законам ла­минарного движения и количественно может быть вычислено по измененной формуле Пуазейля:

Q = _£і=і£і_ „ d^nf мї/сек, 4 128 / p. J і >

Где: q — количество жидкости в м3, прошедшее через капилля­ры (поры), имеющиеся в 1 кг экстрагируемого мате­риала, їв секунду; рі—р2 — суммарная движущая сила проникновения раствори­теля в капиллярах, выраженная в кг/м2. Она, как вид­но, представляет разность гидростатических давлений соответственно в начале и в конце капилляра; d — диаметр капилляров в м; I — длина капилляров в м;

П — число капилляров на 1 м2 поверхности экстрагируе­мого материала; f — удельная поверхность 1 кг экстрагируемого материала; [х — вязкость растворителя в кг~сек/м2; ее можно опреде­лить, пользуясь вязкостью, выраженной в °Е.

Р = ( 7,24Е-^) Ч

Е / g 106

Где у— удельный вес жидкости в кг/м3), g=9,81 м/сек2.

Приведенная формула указывает на факторы, от которых за­висит проникновение растворителя внутрь частицы.

Это прежде всего разность гидростатических давлений (pi—Р2), о которой уже было сказано, что она зависит от ре­жима прокачки и от давления в порах частиц, которое в свою

Очередь зависит от концентрации мисцеллы и от температурно­го режима экстракции.»

Удельная поверхность / зависит от степени измельчения экс­трагируемого материала; длина капилляров I, диаметр их d и число п зависят от способа режима подготовки экстрагируе­мого материала в жаровнях и прессах. Вязкость fx зависит от температуры и концентрации растворителя (мисцеллы). Для

- „ „ „ кФп/

Любой данной твердой системы величина представля-

128/

Ет собой константу К, следовательно, выражение для вязкого потока будет:

V-

Растворение масла, находящегося на поверхностях частицы в свободном состоянии и не связанного, таким образом, сорб - ционно, 'происходит, очевидно, по закону молекулярной диффу­зии в неподвижной среде.

В этом случае скорость растворения масла в растворителе прямо пропорциональна величине "поверхности масляных капе­лек, которая зависит от масличности и характера обмасливания экстрагируемого материала, градиенту концентрации, абсолют­ной температуре и обратно пропорциональна вязкости раствори­теля. Вязкость растворителя уменьшается с повышением темпе­ратуры, следовательно, повышение температуры положительно сказывается на скорости растворения.

Процесс молекулярной диффузии в момент извлечения масла осложняется тем, что различные компоненты жировых веществ неодинаково растворяются в растворителе. Так, оксикислоты. У" жировые кислоты растворяются несколько по-иному, чем три- глицериды. Кроме того, осложнение происходит и в силу на­личия мембран как в виде неразрушенных клеточных стеибк, так и перепонок вторичных структур.

Продвижение масла вместе с потоком мисцеллы изнутри ча­стицы к ее поверхности определяется, очевидно, двумя факто­рами. Во-первых, силами диффузии масла по капиллярам, за­полненными імисцеллой. От каких причин зависит скорость диф­фузии на этих участках, указывалось ранее. Следует только учи­тывать, что поверхностью диффузии в этом случае является сум­ма поперечных сечений капилляров, по которым происходит npoJ движение мисцеллы. Во-вторых, продвижение масла к поверх­ности определяется силами осмотического давления, развиваю­щимися в порах частиц вследствие проникновения в масло па­ров растворителя. Так как в результате осмотического давления мисцелла передвигается по закону Пуазейля, то скорость цир­куляции мисцеллы находится в прямой зависимости от силы

Осмотического давления, структуры и пористости экстрагируе­мого материала, масличности его и от температуры и концентра­ции мисцеллы. Как видно из сказанного, механизм движения масла изнутри частицы к ее поверхности весьма сложен и ко­эффициент диффузии в этом случае является суммирующей ха­рактеристикой внутренней структуры экстрагируемой частицы.

Диффузия масла, вышедшего с мисцеллой на поверхность - частицы к общему наружному потоку мисцеллы, связывается с наличием на поверхности экстрагируемой частицы малоподвиж­ного диффузионного слоя.

Согласно современным представлениям [91, 97], при продви­жении твердой частицы через жидкую фазу (или наоборот) на поверхности частицы образуется диффузионный слой, по толщи­не которого в направлении от его наружной поверхности к по­верхности твердой частицы конвективные потоки затухают, а затем на определенном расстоянии от поверхности частицы и вовсе прекращаются, т. е. в этом месте конвективный перенос вещества равен нулю и, следовательно, протекает молекулярная диффузия. Таким образом, перенос масла у поверхности частицы есть продолжение предыдущего процесса молекулярной диффу­зии внутри частицы, но только в иных условиях. Эта зона назы­вается пограничным или диффузионным слоем. Толщина диф­фузионного слоя зависит от коэффициента диффузии и ддя нее Франц-Каменецкий [91] дает такое математическое выражение:

D

Где: —толщина диффузионного слоя;

D — коэффициент диффузии;

Р —• константа скорости диффузии.

Конвективный перенос масла в поток мис­целлы является >весьма важным этапом про­цесса экстракции, причем в маслоэкстракцион - ном производстве мы сталкиваемся исключи­тельно с вынужденной, а не естественной кон­векцией. Выше мы указывали, от каких факто­ров зависит конвективный коэффициент диф­фузии,

В свете сказанного последние стадии экс­тракции применительно 'К одной элементар­ной частице экстрагируемого материала можно рассматривать следующим обра­зом.

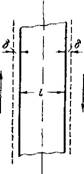
Рис. 22. Механшм экстракции твер­дой частицы.

Представим себе частицу экстрагируемого материала (рис. 22), помещенную в потоке мисцеллы с концентрацией С2, в виде лепест­
ка толщиной I. Тогда, согласно с только что высказанной схе­мой, у поверхности частицы будет образовываться диффузион­ный слой толщиной б.

Обозначая через De, D и р соответствующие коэффициенты диффузии внутри частицы, в диффузионном слое и конвектив­ном участке, через Ct—среднюю концентрацию мисцеллы, нахо­дящуюся на расстоянии Цп от поверхности частицы, через С— концентрацию у наружной поверхности лепестка и через С"— у наружной поверхности диффузионного слоя и предполагая, что для каждого момента установившейся экстракции диффузион­ные потоки q внутри экстрагируемой частицы / £ С \

Q = — De — ], через диффузионный слой <7 = — £> X

\ Цп J 1С С" \

X 1 и в - конвективном участке q =—В (С"—С2) будут

\ Цп ' •

Равны, Белобородов (96, 98], преобразуя все три уравнения отно­сительно С, получил следующее общее уравнение для диффузион­ного потока:

<]= : ; —{Ci — Ct).

I О 1

NDe ' О + р

Так как выражение

+ 1

ND. D ^ р

Есть коэффициенты массопередачи, то в окончательном выраже­нии уравнение для диффузионного потока получает вид

<7=— К(СХ —- С2).

Здесь коэффициент массопередачи К представляет собой ко­личество масла, переносимое в единицу времени через единицу поверхности при разности концентрации, равной единице. Он за­висит от времени, масличности и размера частиц экстрагируе­мого материала.

Анализируя выражение для К, видим, что член ——- по-

ПОв

Называет зависимость его от размера частиц (I) и от внутрен­ней структуры материала, учтенной коэффициентом D g, т. е. от степени разрушения клеточной структуры, пористости и т. п.

Кроме того, De зависит от молекулярного коэффициента диф­фузии масла в растворителе.

Член показывает зависимость К от скорости и режима

Движения мисцеллы и от применяемого растворителя и его тем­пературы.

Член показывает зависимость коэффициента массопере - Р

Дачи от конвективного коэффициента диффузии.

При экстракции гексаном, по данным Коута и Вингарда. [90], коэффициент диффузии (De■ 107 см2/сек) масла внутри частиц: сырого соевого лепестка толщиной 0,279 мм равен 0,136, а тол­щиной 0,533 мм—0,570; сырого хлопкового лепестка толщиной 0,272 мм — 0,176, а толщиной 0,325 мм—0,211.

При экстракции бензином, по данным Белобородова [100], ко­эффициент диффузии масла внутри сырого соевого лепестка толщиной 0,35 мм (D • 106 см2!сек) равен 0,091, а коэффициент массопередачи (К - 105 см/сек) равен 2,38 (при экстракции в те­чение 6 минут)[3].

Выше была представлена схема экстракции применительно к одной изолированной частице экстрагируемого материала. При экстракции материала в слое на скорость ее будет ока­зывать влияние слеживание частиц и блокирование их наруж­ной поверхности, причем слеживание это может происходить как за счет веса столба частиц, так и за счет напора движу­щегося растворителя. Помимо слеживания, движение через слой растворителя может приводить к заносу нижних участков слоя мелкими частицами, уносимыми потоком растворителя из верх­них участков. Это в свою очередь будет вызывать неравномер­ную прокачку отдельных частиц в силу того, что растворитель будет протекать по участкам наименьшего сопротивления.