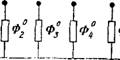ГИДРО­ГЕОЛОГИЧЕСКИЕ ИССЛЕДОВАНИЯ НА ОРОШАЕМЫХ ТЕРРИТОРИЯХ

Структура моделей

В геофильтрационных расчетах на орошаемых территориях ос­новными структурными типами потоков являются плановые потоки или системы плановых потоков, соединенных по схеме перетека­ния. Моделирование таких потоков производится на сплошных, сеточных и комбинированных моделях, а также на ЭЦВМ, которые в последнее время получают все большее распространение для геофильтрационных расчетов. Контуры внешних и внутренних гра­ниц модели определяются гидродинамическими границами, обо­снованными при геофильтрационной схематизации (при этом спе­циального обоснования требует задание граничных условий при использовании принципа суперпозиции [17]).

При разбивке сеточных моделей следует исходить из общих по­ложений дискретизации поля, изложенных, например, в работе [17]. На практике рекомендуется в пределах каждой области с раз­личными параметрами по любому ее сечению иметь не менее двух - трех блоков. Кроме того, вблизи зоны возмущения потока нужно иметь не менее трех-четырех блоков в пределах минимальной об­ласти влияния, для чего шаг сетки а вблизи области возмущения

Должен удовлетворять неравенству ее (1-И,5) д/а^ііп, где кпіп—минимальное расчетное время протекания исследуемого про­цесса.

При дискретизации поля потока наибольшее распространение имеют прямолинейные ортогональные сетки. Представляет интерес также использование криволинейных ортогональных и нерегуляр­ных треугольных сеток [17], позволяющих наиболее гибко приспо­собить модель к особенностям моделируемого потока.

При моделировании отдельных горизонтальных дрен учет их гидродинамического несовершенства осуществляется подключением дополнительных сопротивлений, на которых реализуется условие (3.9). На сеточных моделях при реализации этого условия пред­полагается, что средний уровень в блоке соответствует уровню на линии дренажа Ял - Построение моделей по такому принципу по­дробно описано в работе [17].

При реализации на сеточной модели густой сети горизонталь­ного дренажа, когда в пределах одного блока располагается не­сколько дрен, правильнее считать расчетный напор в блоке соот­ветствующим среднему напору между дренами. В этом случае в блок с дренами вводится дополнительное сопротивление ФДр, на конце которого задается напор воды в дрене Яд. Исходя из того, что в блоке установился средний уровень на междудреньи, вели­чина Фдр определяется по формуле

(3.21)

Где Z-др — общая протяженность линейных дрен в пределах блока; L — расстояние между дренами; £д— параметр сопротивления, обусловленного несовершенством дрены.

Для региональных оценок баланса подземных вод в блоке с дренами можно задавать средний напор в пласте Я*, считая его по выражению Я* = 7з(2ЯсЧ-Яд), где Н°—напор посередине между дренами. Этот способ целесообразно применять, в частно­сти, при многопластовом строении водоносного комплекса для определения на модели внешнего притока, поступающего к дре­нажу из нижележащих напорных пластов.

При геофильтрационном моделировании водозаборов и дрена­жей в слоистых системах, характерных для предгорных и межгор­ных отложений, целесообразно сочетать профильные и плановые модели, используя для этого следующие пути решения.

В первую очередь рассматриваются профильные задачи для ленты тока, выделяемой по генеральному направлению потока, со-

А

"/чЧЧЧЧЧЧ

Г н'-н'9 Н^Н;

ЕЗ/ ПЗг CZUj

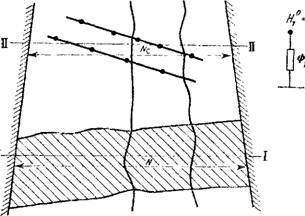
Рис, 40, Схемы, иллюстрирующие переход к профильному потоку при моделиро­вании водоотбора на участке конусов выноса.

Й —план поверхности участка; б —профиль поверхности земли по сеченню 1-І; в — система фильтрационных сопротивлений дрен и водотоков (рек) по сечению 1-І; г — сопротивления водотоков и задание суммарного расхода водозаборных скважин по сеченню ІЗ— II; 1 — зона выклинивания потока в систематический горизонтальный дренаж; 2 — водотоки; 3 — водозаборные скважины; 4 — боковые границы потока, проводимые по лнииям тока между водозаборными участками в соседних конусах выноса

Впадающему обычно с направлением падения поверхности земли. Такая расчетная лента может иметь переменную ширину, занимая всю межгорную долину или ограничиваясь в предгорных отложе­ниях одним или несколькими слившимися конусами выноса. При этом в каждом сечении фильтрационные сопротивления и емкости находятся применительно к средней ширине потока, задаваемые значения расхода потока (инфильтрации, выклинивания, водоот­бора) суммируются, а фйльтрационные сопротивления водотоков и дрен на поверхности земли складываются по правилам сложе­ния параллельных сопротивлений. При наличии нескольких (п) та­ких сопротивлений Ф®. (рис. 40) суммарное сопротивление Ф°

Определяется из соотношения
где Щ — напоры, задаваемые на концах сопротивлений Ф° (в во­дотоках и дренах). Расположение водозаборных и дренажных скважин представляется в форме рядов или площадок, распреде­ляемых по всей ширине N с расчетной ленты тока.

Получив на такой модели напор в скважинных блоках, следует далее переходить к напору в скважине Яс по соотношению (3.2) при Ял, равном напору в блоке, и расчетном расстоянии между скважинами a — Ncjnc, где пс — число скважин в данном ряду. Для площадных систем такой переход проводится по соотноше­нию (3.17).

На таких моделях получают в первом приближении решение серии прогнозных и разведочных задач, по данным которого тща­тельно анализируется структура баланса потока и выявляется роль каждого из пластов в формировании потока. Если при этом оказывается, что нижние пласты несут небольшой расход потока, то их можно исключить из расчетной схемы.

Следующий этап решения таких задач осуществляется на пла­новой модели, на которой проводимость и емкость принимаются суммарными для всех пластов. Сопротивления поверхностных водо­токов и дрен задаются из условия, чтобы общее вертикальное со­противление профильного потока между поверхностными водото­ками (дренами) и водозаборами соответствовало сопротивлению Ф° , задаваемому по водотокам на поверхности планового потока.

Сопротивление Ф« профильной л-слойной модели (рис. 41, а) на­ходится при стационарном режиме с заданием на поверхности по­тока напора Я0, через сопротивления водотоков (дрен), при этом

На линии водозаборов задаются совершенные дрены с одинако­выми напорами Н'0= Н"0 = ... — Я0 (на электрической модели на­порам Но и Я0 соответствуют относительные потенциалы П = 1 и 0 = 0) и дополнительными сопротивлениями Ф°. = 0. В соответ­ствии с ранее обоснованными рекомендациями [17] шаг сетки за­дается с соблюдением условия Ах ^ 0,45 (с допускаемой погреш­ностью 5%), причем для трехпластовой системы можно считать

Общее сопротивление такой л-слойной модели Ф° находится по­сле замеров напоров (потенциалов) в узлах первого столбца (бли­жайших к водозаборным узлам) из соотношения

(3.23)

Где AC/^(AC/q5, АС/'о, , ...) —значение разницы относительных по­тенциалов между узловыми точками нулевого и первого столбцов на каждой г'-й строчке. После этого на линейной модели планового

Потока при Ф0 = 0 (см. рис. 41, б) подбираются значения Фсп так,

Чтобы на первом сопротивлении (Фі) получилась разница относи­тельных потенциалов А£70і = Фі/Ф°

Если значения напоров задаются на поверхности земли по всей длине потока, то при использовании принципа суперпозиции сле­дует под Я понимать изменения напора по отношению к уровням естественного потока. Тогда Я° — 0 и величина Ф° может быть

І п

Получена аналитически по формуле о (Ф І?™

= (3.23а)

Где Ах— шаг сетки; N— принятая ширина профильного потока.

После этого расчетные значения сопротивлений водотоков (дрен) Ф°в, задаваемые для планового потока, пересчитываются

Из исходных сопротивлений водотоков Фв по соотношению

Ф° /Фв==Ф°эт/Фп.

Следующим этапом обоснования плановой модели является расчет обобщенного дополнительного сопротивления Фо с учетом реального расположения водозабора. Для этого на профильной многослойной модели задается реальное распределение ряда водо­заборных скважин, причем для ряда скважин в i-u пласте допол­нительное сопротивление Фо, находится при Т=Ти а в пластах, где отсутствуют скважины, задается Ф0=оо. В такой постановке находится сопротивление многослойной модели Ф„ так же, как Ф° —ИЗ соотношения (3.23), после чего имеем Фо==Фп — Ф°м-

Соответственно параметр сопротивления контура скважин £кс = = TN СФ0.

При необходимости более детального анализа пространствен­ной структуры многопластового потока следует переходить к двух - пластовой модели, профильный аналог которой приведен на рис. 41,в. В этом случае в первую очередь на профильной модели получается суммарное сопротивление Ф° (при одинаковых значе­ниях напоров Щ), по которому подбирается удельное сопротивле­ние разделяющего пласта tnp/kp двухпластовой модели из условия эквивалентности суммарного сопротивления Ф°п. Если во всех уз­лах расчетные величины напоров Я° = 0, то расчетное значение параметра mp/kp определяется согласно аналитическому решению (см. прил. 1) подбором из соотношения (46).

Если водоотбор осуществляется только из нижних пластов, то при переходе к двухпластовой модели определяется также допол­нительное сопротивление водозабора Ф". Для этого при реальном

Расположении водозабора в л-пластовой системе находится сум­марное фильтрационное сопротивление Ф«, по которому рассчиты­вается Ф^==Ф„ —Ф2, где Ф2 —сопротивление водозабора, распо­лагаемого в нижнем пласте двухпластового потока, его величина определяется выражением (48) в прил. 1.

2. Переменные граничные условия

Существенные затруднения возникают при задании на емко­стных моделях переменных граничных условий, поскольку в этом случае автоматическое задание переменных граничных условий тре­бует применения довольно сложной аппаратуры. При решении ис­ходных уравнений в линеаризованной постановке (с постоянными параметрами) заметное упрощение учета переменных граничных условий достигается использованием временной суперпозиции. По этому способу для задания переменной во времени границы I рода предварительно производится моделирование с постоян­ным граничным условием при относительном потенциале на гра­нице U — 1 (100%). Получаемое при этом распределение потен­циала^ на модели представляет собой исходную единичную функ­цию U\(t). Если далее требуется получить решение для любого граничного условия, описываемого функцией f(t), то ее можно аппроксимировать ступенчатым графиком и записать решение та­кой задачи на основании принципа суперпозиции [17].

Аналогично можно произвести моделирование и для перемен­ного граничного условия II рода. В этом случае исходная единич­ная функция находится при единичном расходе потока (силе тока) на границе. Обычно условия заданного расхода потока устанавли­ваются внутри области потока, представляя собой, таким образом, внутренние источники-стоки. Особенности моделирования рассмат­риваются ниже особо.

При изменении граничных условий по контуру границы по­следний разбивается на ряд участков, в пределах которых гранич­ное условие можно считать одинаковым, после чего решение на модели и последующие расчеты производятся для каждого уча­стка в отдельности, а затем результаты этих расчетов склады­ваются.

Своеобразные сложности возникают при задании периодиче­ски меняющегося граничного условия, имеющего обычно внутриго - довую периодичность (например, при сезонных колебаниях уровней водохранилища, суточных, недельных и месячных изменениях де­бита водозаборных скважин, при поливах на орошаемых террито­риях), когда многолетние и внутригодовые изменения граничных условий имеют различный порядок во времени. В этом случае целе­сообразно расчленить периодический график граничного условия на многолетний и внутригодовой, причем последний рассчиты­вается только на один-два годовых цикла [17, 38]. Такое моделиро­вание обычно приходится проводить в два этапа—для многолет­него и внутригодового режима,—выбирая различные масштабы времени применительно к условиям многолетнего и внутригодового графиков граничных условий.

Особого обоснования требует учет периодичности работы оро­сительного канала при подпертом режиме фильтрации, для кото­рого характерно изменение рода граничного условия в период от­ключения канала (в этом случае условие III рода переходит в усло-
виє II рода), так что при этом возможность применения принципа суперпозиции исключается.

При постановке такой задачи требуется прежде всего устано­вить критерий смены рода граничного условия под каналом. Та­кой критерий четко устанавливается для экранированного русла канала, когда свободная фильтрация имеет место при расположе­нии уровня грунтовых вод ниже поверхности канала, а подпертая фильтрация — при подпирании уровнем грунтовых вод подошвы экрана. Таким образом, в этом случае смена рода условия под каналом наступает при прохождении уровня свободной поверхно­сти потока через отметку подошвы экрана.

Несколько менее определенно решается этот вопрос при отсут­ствии экрана в русле канала, поскольку в этом случае при колеба­ниях уровня под каналом переход от подпертого режима к сво­бодному и наоборот осуществляется постепенно.

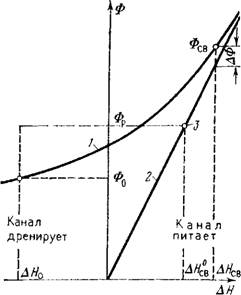
При реализации таких условий фильтрации из водотока на электрической модели или на ЭЦВМ необходимо аппроксимиро­вать нелинейную зависимость q от АН какой-либо функцией, при­чем наиболее удобными являются сочетания граничных условий II рода (q = const) и III рода (Ф = const). Опорными для по­строения аппроксимирующего графика являются начальная точка, определяющая сопротивление Ф0 при исходной разнице напоров АНо, и разница напоров АЯСВ, при которой фильтрация из водо­тока может считаться свободной с допустимой погрешностью дд — = ДФ/Фсв (рис. 42). Наиболее простая форма аппроксимирую­щего графика получается путем задания условия III рода при АН > АЯсв и условия II рода при АН АЯСВ. При такой аппрокси­мации расчетное сопротивление ложа водотока Фр можно зада­вать равным осредненному зна­чению в пределах между значе­ниями, соответствующими разни­цам напоров АЯо и АЯсв, в этом случае смена условий II и III ро­да производится при разнице на­поров АЯСВ. Более обстоятельный выбор применяемого расчетного приема в таких условиях должен производиться на основании ре­зультатов тестовых расчетов.

Заметим, что характер пере­хода свободной фильтрации в подпертую может существенно зависеть от неоднородности строения отложений под водото­
ком, однако характер и пути выявления такой зависимости пока остаются не определенными.

Для приближенного расчета периодичность работы канала при подпертой фильтрации можно учесть, вводя фиктивное (расчетное) значение параметра сопротивления ложа канала L* (или AL*).

Значение L* определяют путем сопоставления результатов тесто­вого моделирования для периодически действующего канала с па­раметром сопротивления LH и расчетов для постоянно действую­щего канала с параметром L* из условия практического совпаде­ния среднегодовых расходов потока, фильтрирующегося из канала.

Для обоснования такого расчетного приема были использованы данные С. Д. Каца по моделированию одномерного нестационар­ного потока в случае работы канала половину времени года при пренебрежимо малом времени промачивания зоны аэрации под ка­налом. Модельные изменения уровней под каналом АН0 с пара­метром сопротивления ложа 1н сопоставляли с расчетными значе­ниями при постоянно действующей границе III рода с параметром сопротивления L*, величина которого находилась из уравне­ния [25]

« F0 (в) = 1 - е02 erfc0; Є = (3.24)

Расчетные моменты времени в (3.24) задавались посередине периодов подъема и спада уровней, что обеспечивало равенство среднегодовых значений модельных и расчетных изменений уров­ней под каналом. Такие расчеты показали, что значения расчетных параметров оказываются практически стабильными во времени и при рассмотренной полугодовой работе канала они могут опре­деляться по аппроксимационной формуле

L* = 4,8 (LH + 0,1 уat(3.24а)

При jfi = 365 сут. Проверка таких расчетов для других сечений и при различной длине потока дала хорошее согласование модель­ных и расчетных данных, что свидетельствует о независимости та­кого расчетного приема от границ и строения потока.

При любой другой периодичности работы канала для такого расчета следует предварительно провести моделирование одно­мерного нестационарного потока в течение трех лет при длине по­тока, равной характерному расстоянию от канала до границ по­тока. После этого вычисляется среднее значение изменения уровней под каналом в пределах третьего года, которое приравнивается значению F0 (б) при t — 2,5 года.

Для решения линеаризованных уравнений нестационарной фильтрации в ряде случаев эффективным оказывается использова­ние интегрального преобразования исходной функции (напора или его изменения) по Лапласу—Карсону. Рекомендации по использо­ванию этого преобразования для геофильтрационных расчетов и моделирования приведены, например, в [17, 38].

Учет начального распределения напоров при неизменных пара­метрах пласта, когда исходные дифференциальные уравнения яв­ляются линейными, целесообразно проводить, вводя в качестве рас­четной функции вместо напора Я его изменение S относительно начального напора Я0 в каждой точке. При этом величина 5 моде­лируется при интенсивности инфильтрации, равной разности зна­чений на прогнозный период и начальный момент времени, а при неизменном инфильтрационном питании изменения напоров 5 не зависят от инфильтрационного питания, причем начальное условие для величины 5 будет нулевым [38].

В общем случае величины Но, от которых отсчитываются рас­четные изменения уровней S, могут быть переменными во времени, однако они, разумеется, долж;ны быть известны в течение всего расчетного периода времени. С этой точки зрения наилучшими яв­ляются такие условия, когда исходные уровни Но задаются при стационарном режиме. Достаточно определенными представляются исходные условия, когда уровни Я с периодически изменяются в те­чение каждого года, и такие периодические изменения могут быть продолжены на расчетный период времени, причем для задания исходных уровней обеспеченности могут быть использованы ста­тистические методы прогноза режима естественного потока.