ГИДРО­ГЕОЛОГИЧЕСКИЕ ИССЛЕДОВАНИЯ НА ОРОШАЕМЫХ ТЕРРИТОРИЯХ

НАЛИВ В УДЛИНЕННЫЙ КОТЛОВАН (ТРАНШЕЮ)

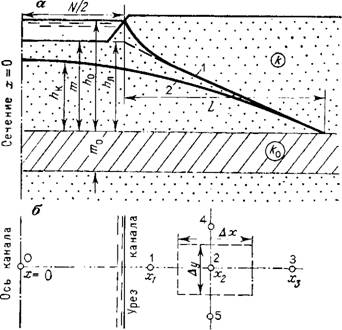
Одним из способов проведения крупномасштабного опробова­ния зоны аэрации является налив в удлиненный котлован (тран­шею), имитирующий опытный участок канала (рис. 58). Сущест­венный недостаток этого способа — значительные потери воды на насыщение зоны аэрации. Поэтому такой опыт целесообразно про­водить только при сравнительно небольшой мощности опробуемой зоны аэрации. В частности, определенный интерес эта схема опро­бования представляет для условий, когда покровные отложения имеют сравнительно небольшую мощность и значительно меньшую проницаемость в нижней части, а уровень грунтовых вод распола­гается ниже их подошвы. В этом случае под опытным отсеком об­разуется своеобразный поток растекания, который в начальный период имеет нестационарный характер, а затем стабилизируется. Для интерпретации опытных данных целесообразно использовать главным образом данные стационарного режима, для которого мо­гут быть составлены сравнительно простые расчетные зависимости.

При выводе зависимостей поток делится на два фрагмента — под каналом и вне его, причем поток под каналом следует раздельно рассмотреть для ус­ловий подпертой фильтрации из канала.

При k^ko и относительно большой ширине канала поток под ним можно описывать, исходя из предпосылок перетекания. В том случае в каждом сече­нии под каналом балансовое уравнение будет

-$r=vK-vn, (4.21)

Где q — расход горизонтального потока; vK и vn — скорости вертикальной фильтрации из канала и через слабопроницаемый слой. Для этих величин при

Подпертой фильтрации из канала можно записать выражения

L. Ш1 «_ 11 П /а

-km-j--, vK = k —------------------- , Un=Јo—0-, (4.22)

Ах тг МІ

Где Я — расчетный напор в верхнем слое; т7 — расчетный путь вертикальной фильтрации в верхнем слое; тй+-~(т—т7) — расчетная мощность верти­кального потока из верхнего слоя через нижний. Подставляя эти выражения в (4.21), получим дифференциальное уравнение для распределения средних на­поров под каналом

, dm. . //0-Я . ь И

Km + k-- ™ Н ko —0 (4.23)

Dx2- тг щ '

Или

+ ------------- L_. (4.24)

Dx2 ттг mmz k тто s '

Общее решение этого уравнения

Н=-^^-- + СїС\ІЬх + С2В\ІЬХ, (4.25)

Где Сі и Сг — произвольные интегрирования, которые находятся из граничных условий. Так, из условия на оси канала dH/dx—0 при дс = 0 и из условия Я= —кл + Шй при x=0,5N получаем

НО

(Лл + я*о) — -L*mm -

Со=0, С\=--------------------------- ь¥ (4.25а)

Ch~2~

Расход потока qK в сечении уреза канала при этом будет dH

——Cikmb sh = x=0,S N 2

Mттг -(/іл-то).

Для определения расчетной мощности тг сопоставим (4.26) с выражением для расхода из канала неограниченной ширины (N-*-оо) при feo=0, тогда оно принимает вид

QK=km (h0 ~ Ал) д/(4.26а)

Л] ттг V тг

Вместе с тем строгое решение такой задачи дает

Сопоставляя (4.26а) и (4.266), получим У ль/т-0,44 или тг = 0,2т. Тогда вы­ражение (4.26) принимает вид

QK=kmb th р (---------------- ^L^— — НЛ — щ\ (4.27)

5 ^ = m +0i8^m) (4.27а)

Т0 к z

Сопоставление со строгим решением для однородного потока на водоупоре по­казывает, что это решение дает приемлемые результаты при А/^ 0,5т.

При малом размере канала для расхода бокового потока можно прини­мать сопротивление потока таким же, как для потока на водоупоре (при k0— = 0), а для расчета потока, фильтрующего под каналом через слабопроницае­мый слой считать средний напор под каналом, равным среднему напору иа ли­нии уреза канала.

Тогда выражения для расходов потока под каналом будут

_ __ ,т Ао — Лл о__________ HhnN оя,

Чк Km, <7к=-2^~. (4.28)

Где &L — сопротивление канала по отношению к верхнему слою. В частности, при однородном строении ложа канала с небольшой глубиной воды и N>2m можно считать [25]

AL =0,44 + 0,16-^-. (4.28а)

Т 1 """ N

Рассмотрим теперь поток во внешнем фрагменте, где также принимаются предпосылки перетекания и глубины потока описываются уравнением

Решение этого уравнения будем искать методом интегрального баланса, зада­вая линейное распределение глубин потока

Л (l---------------- (4.30)

Подставляя (4.30) в (4.29), получим приближенное равенство Ал

(4-31)

L2 - то

Которое будем выполнять, интегрируя его от 0 до L, что дает

-£--£-(4-+4 <«•*>

Причем

H

(4.32а)

Для получения полных фильтрационных потерь из канала большой ширины следует еще добавить расход q^, фильтрующийся через слабопроницаемый слой под каналом

N12 ЛГ/2

О Г Hdx=J<L Г =

К т j т0 Jn \ ЬШтг ^ 1 )

(--------- * + - Ал - moV ■ (4.33)

Суммарный погонный расход фильтрации из канала <7K=2(g,®+<7К), со­гласно (4.27) и (4.33), можно записать в виде

2

Л (4.34)

То ).

Р

Где обозначено

__ к+М______ (4.34а)

Щ +0,67km ' >

Аналогично решается эта задача при свободной фильтрации из канала, когда для qK можно записать выражение

Fti h„ - f - тп

Fc—^ + W-^-*.. (4.35)

Где hK —средняя глубина потока под каналом.

При проведении опытного налива в такой канал (котлован) замеряется расход фильтрации из канала QK, по которому нахо­дится удельный расход qK = QK/2lK, где /к — длина опытного уча­стка канала. Как показывают данные практических замеров, ве­личина удельного расхода из канала может существенно меняться по его длине. Для контроля за неравномерностью фильтрации из канала целесообразно замерять потери в канале по нескольким отсекам.

Наблюдательная пьезометрическая сеть задается по створу по­перек канала с дополнительными скважинами поперек створа (см. рис. 58, б). Желательно эти скважины устанавливать на пол­ную глубину верхнего, более проницаемого слоя. По замерам в этих пьезометрах устанавливается зависимость глубины потока h от расстояния до канала х, которая согласно (4.30) принимается ли­нейной. По точкам на графике h (х) проводится прямая линия, от­секающая значения h = hn при х=0 и x — L при h — 0. Тогда можно получить соотношение коэффициентов фильтрации

= (4.36)

(-W-+1)"

После чего рассчитать qK по выражениям (4.34) или (4.35) и по­лучить k = qK/qK.

Обработку данных нестационарного режима при свободной фильтрации из канала можно проводить, пользуясь конечно-раз­ностными уравнениями, составляемыми для блока площадью Ах А у за интервал времени At внутри «креста» пьезометров (см. рис. 58, б)

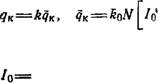
+ h5AxI5)=ko + (4.37)
где Ах и Ау—размеры блока, причем Ах равно половине расстоя­ния между пьезометрами I я 3, а Ау равно половине расстояния между пьезометрами 4 и 5; hs, /м, Нь— средние глубины потока между пьезометрами 3, 4, 5 и 2; hi— средняя за интервал At глу­бина потока по пьезометру 2; АЛг — изменение уровня воды в пье­зометре 2 за время At; ho і и Д/toi — глубина потока и изменение уровня воды за время At, средние по пьезометрам 0 (ho) и 1 (hi), причем

ДАо1 + АЬ_(х2-хі) = L. (4.37а)

Х2 + Х1 Х2"Ь*1

Для упрощения записи представим уравнение (4.37) в виде

Где vh и /п — средние значения скорости подъема уровней и гра­диентов напора в подошве; М3 иМ — модули расхода фильтрации из канала и изменения расходов в расчетном блоке

О X] , ' Х2 — XI. " , . ОЛ,

VH=V% — + VH _2-_ + «Я. (4.38а)

TOC \o "1-3" \h \z / — і a - + Х2 - J - + /го*' +0,5fti (Х2 — х\) . g,

П 2Д* то Ах ' \ • )

M^-l^, (4.38s)

9 Ах Ay Ах Ay х '

В уравнении (4.38) три переменные и поэтому его использова­ние для определения всех трех параметров требует дополнительной информации. Если, например, найдены значения k и ко по стацио­нарному режиму, то из уравнения (4.38) определяется величина р. Если же в процессе опыта замеряется изменение влажности, по ко­торому можно установить величину р, то уравнение (4.38) пере­писывается в виде

Hut, — Мл /„

K=*koZ2 + Zu = (4.39)

Составляя по опытным данным график зависимости величин Z\ и Z2, в соответствии с уравнением (4.39) должны получить на этом графике прямую линию, отсекающую на осях Z\ и Z2 значения Z\=k и Z\= kjkо.

При таких расчетах следует очень внимательно относиться к обоснованию величины qK, учитывая, что заметная часть потерь из канала может тратиться на изменение влагозапасов в зоне аэра­ции, а также считаясь с возможной неравномерностью фильтрации по площади опытного участка канала (котлована).