ФИЗИКА ЖИЗНЕННЫХ ПРОЦЕССОВ

ТЕОРИЯ ДОБИОЛОГИЧЕСКОЙ ЭВОЛЮЦИИ

Основные проблемы, с которыми имеет дело теория добиоло- гической эволюции, это проблема возникновения самооргани­зующихся полимерных систем из первоначальной хаотической смеси различных мономеров и проблема последующей эволюции таких систем. Сходные проблемы фигурируют и в теории биоло­гической эволюции — самоорганизация клеток и многоклеточ­ных организмов и необходимое их эволюционное развитие в ре­зультате естественного отбора. Решение этих проблем требует преодоления принципиальных трудностей, столь значительных, что и сегодня оно многим представляется невозможным. Оче­видно, что либо эволюция должна начинаться со случайных со­бытий, либо должны были существовать акты творения — один или несколько. Случайную самоорганизацию хаоса и возникно­вение необходимой эволюции трудно себе представить. Эта труд­ность воспринимается как аргумент в пользу креационизма, в конечном счете, как научное доказательство бытия божьего (см. например [42]). В самом деле, число различных полину- клеотидных цепей длиною в 100 звеньев, построенных из четы­рех нуклеотидов, равно 4100 » 1060. Случайный выбор нескольких определенных полинуклеотидов из такой смеси (которая должна даже при плотной упаковке занимать объем, на много порядков больший Мирового океана) имеет ничтожную вероятность и, следовательно, не реализуем.

Однако физика открыла пути для преодоления этих труд­ностей. Изложенная в гл. 8 термодинамика нелинейных нерав­новесных процессов доказывает принципиальную возможность возникновения систем, упорядоченных в пространстве и вре­мени, в гомогенной, т. е. хаотической среде. Условием возникно­вения порядка в открытой системе является наличие автоката­литических процессов и обратных связей.

Исходя из этих идей, Эйген предложил модельную теорию самоорганизации и эволюции биологических макромолекул [43, 44]. В настоящем параграфе и в последующих мы приводим краткое изложение теории Эйгена (см. также [83—87, 170]).

Эйген рассматривает «ящик» конечного объема V, имеющий стенки, проницаемые для высоко - и низкоэнергетических моно­меров, но не для полимеров. Внутри ящика происходит полиме­ризация и деполимеризация. Образуются и распадаются инфор­мационные макромолекулярные цепи, обладающие различной первичной структурой. Количество цепей в 1 см3, содержащих v звеньев, число сортов которых равно X (для нуклеиновых кислот % = 4, для белков X — 20), с последовательностью звеньев за номером k равно хчн - Общее число цепей длины v в единице объема равно

(9.1)

Где Nv — Для большинства из Nv возможных информацион­ных цепей их концентрации xvh равны нулю. Концентрации сво - бодиых высокоэнергетических мономеров в ящике равны т\,т2, ..., тх, а их потоки в ящик Фь Ф2, ..., Фх. Число всех единиц — свободных и полимеризованных — равно

К

TOC \o "1-3" \h \z М0 = £ mt + £ vnv. (9.2)

1=1 V

Очевидно, что полная численность цепей данной длины v в объеме V очень мала по сравнению с возможным числом Nv таких цепей, обладающих различной первичной структурой:

NvV < Nv. (9.3)

Для v = 100, X — 20 имеем Nv ~ 10130. При любых разумных значениях V неравенство (9.3) соблюдается. В отсутствие само­инструктирования, т. е. фактора отбора, ожидаемое значение числа цепей с любой данной последовательностью практически равно нулю.

Ящик Эйгена открыт и далек от равновесия. Он снабжается свободной энергией, например, в виде богатых энергией моно­меров. Самоорганизация возможна, если полимеры обладают автокаталитическими свойствами, т. е. способны к репликациои - ному матричному синтезу. Необходимое условие самоорганиза­ции состоит в том, что скорость полимеризации должна превы­шать скорость распада и иметь по меньшей мере тот же поря­док по xvh.

Напишем простейшее кинетическое уравнение для каждого носителя информации, учитывая мутабильность, т. е. возмож­ность неточного копирования. Имеем

*t = FiXi — RiXt + £ фцхи (9.4)

ІФІ 4 '

Где первый член описывает скорость самоинструктированной сборки цепи, второй — скорость убывания числа цепей посред­ством их распада и разбавления. Третий член описывает воз­никновение і-х цепей вследствие неточного копирования других, близких 1-х последовательностей. Параметр Ft зависит от кон­центраций мономеров гп\, ..., т^. Уравнения (9.4) нелинейны, так как /ч и Ri могут зависеть от х{ и от Хк (к ф і). Введя кон­станту скорости k0, измеряемую в с-1, напишем

Fi = k0 AiQ{, R{ = k0D{ + фог. (9.5)

Произведение AiQi описывает скорость образования і-й цепи; At — фактор усиления, Qi — «фактор качества» — число, показы­вающее, какая доля процессов матричного синтеза дает точные копии носителя информации и. Доля 1 — Qi отвечает образова­нию мутантов ij. Произведение AiQi зависит от концентраций мономеров и, если они поддерживаются постоянными, то можно написать

Лгдг = /(т„ ..., тк) АЩ. (9.6)

Член D{ описывает распад цепей, а ф0г — уменьшение их кон­центрации вследствие разбавления. В простейшем случае фо» связано с общим потоком разбавления Ф0 соотношением

Фо = Фо/Е хк. (9.7)

K=i

Индекс і в этом случае можно опустить. Тогда уравнения (9.4) принимают вид

Xi = k0 (AiQi — D;) ХІ + фttxi — Фо(9.8)

Уравнения (9.8) описывают метаболизм, характеризуемый сум­мами k0 £ DtXi и k0 X A[Xlt самовоспроизведение и мута - бильность, выражаемую фактором качества Q, < 1. Носители информации, для которых AiQi > D{, увеличиваются в числе, а те из них, для которых AiQi < вымирают. Тем самым, про­исходит сегрегация, разделение системы на две части, но еще не отбор. Для отбора должны существовать селекционные огра­ничения.

Ограничения, обеспечивающие селекцию, могут налагаться условием стационарности. Допустим, что общая организация си­стемы постоянна. На языке термодинамики это означает по­стоянство обобщенных сил, т. е. концентраций мономеров и по­лимеров. Ограничения имеют вид

Ти т2, ..., тК = const, f(mu т2, ..., тк) = const,

" (9.9)

2j Xk — n = const. fe-1

Одновременно поток разбавления Ф0 таков, что он компенсирует суммарную избыточную продукцию информационных цепей

N

Фо=*оЕ (Ak-Dk)xk. (9.10)

Альтернативное селекционное ограничение может состоять в по­стоянстве не сил, а потоков. Введем теперь определения

Е{ — At — Dt — продуктивность, (9.11)

_ N N

Е — X EkxdH xk~ средняя продуктивность, (9.12) Wi — AiQi — Di — селективная ценность. (9.13)

Учитывая (9.7) и (9.10), перепишем уравнения (9.8) в виде

Xi = k0(Wi — E)xi+ Еф itxt. (9.14)

Іфі '

Уравнения (9.14) существенно нелинейны, так как Е содержит все Xh■ Этот член дает скользящий и саморегулируемый порог самоорганизации. Увеличивается число лишь тех носителей ин­формации, селективные ценности которых Wi выше порога П. Увеличение их числа сдвигает порог Е в сторону все больших значений, пока не будет достигнут оптимум Е, равный макси­мальной селективной ценности Wm всех имеющихся видов

Ё-* Wm.

Следовательно, система будет стремиться к состоянию «селек­ционного равновесия», являющемуся, однако, неустойчивым. Оно нарушится при появлении вследствие мутаций новой копии іт+ь обладающей более высокой селективной ценностью, т. е. отвечающей условию Wm+1 > Wm. При этом система перейдет в новое состояние равновесия и т. д. Оптимизация такого рода может быть немонотонной, так как максимум селективной цен­ности Wm зависит от данного распределения концентраций характеризующего условия среды.

Введение селективной ценности (9.13) должно означать вве­дение ценности информации, выражаемой через реальные физи­ческие величины и характеризующей скорость размножения це­пей (ср. стр. 514).

В термодинамическом смысле каждая мутация, ведущая к дальнейшему росту селективной ценности, соответствует отри­цательной флуктуации производства энтропии и указывает на неустойчивость существующего стационарного состояния.

Среднюю продуктивность (9.12) можно представить в виде

Етхт+ EЈft*ft £= *±JH = Екфт Ч {Ещ Ek^m)t (9.15)

Zj xk

Где

Екфт= Е ЕкХт/ Е Xk (9 16)

Кфт ' кфт v >

N

Выражает среднюю остаточную продуктивность, причем Е xk=n,

К= 1

Е Хк — п — хт. Условие равновесия E — Wn дает «равновесную

Кфт

Долю» отобранного вида, т. е. его относительное выживание

Хт ^т ~ Екфт

Эта величина не пропорциональна Qm, но стационарная ошибоч­ная доля 1 — хт/п пропорциональна 1 — Qm'

= (1 — Qm)- (9.18)

П т Ыфт

При Qm — 1 Хт — п, т. е. произошел бы полный отбор «главных копий» іт, но дальнейшая эволюция прекратилась бы. Для эво­люции необходимо значение Qm, меньшее 1, но большее неко­торого минимального значения Qmin, при котором выживание еще возможно. Значение Qmin находится из условия хт = 0, т. е. Wm = Еифт. Имеем __ _

1 > Qm>Qmla=AkҐ"n + DAm~Dk*m. (9.19)

Влияние фактора Qm на процесс отбора состоит в том, что он приводит к большему разнообразию мутантов и, значит, позво­ляет прийти к большему конечному оптимальному значению Wm, а также увеличивает скорость эволюции. Общий критерий от­бора, согласно (9.17), есть

Wm > Ёкфт, (9.20)

Что может быть осуществлено через посредство каждого из пара­метров в зависимости от наложенных условий.

Фактор качества Q определяется точностью узнавания звена данного сорта при матричной редупликации (см. § 1.2). Простей­ший случай соответствует некооперативному узнаванию, т. е. мономер, включаемый в новую цепь, узнается лишь одним зве­ном старой цепи, причем имеются лишь две возможности — мо­номер комплементарен или не комплементарен звену. Если ве­роятность точного воспроизведения отдельной единицы есть q, то вероятность образования безошибочной копии, содержащей v звеньев, есть

Q=QVa = q\ (9.21)

Математическое ожидание ошибки в цепи из v звеньев равно

Е — v(l — q).

Распределение вероятностей для возникновения цепи с k ошиб­ками биномиально:

При £(1—<7)^1 оно аппроксимируется распределением Пу­ассона

Л — Efe ехр (— е) _ у* (1 — G)K ехр [— у (1 — <?)]

ы й •

Следовательно, вероятность возникновения безошибочной копии Qv0 = exp[— v(l — <7)]

Убывает с ростом длины цепи v. Минимальное значение Qvо при данном значении фактора узнавания q дается условием

(9.24)

V < І ІП Qmin 1/(1 - q),

Т. е. максимальное количество информации, пропорциональное Vmax и сохраняемое в процессе воспроизведения при данном q, есть

Очевидно, что в ходе эволюции должен улучшаться элементар­ный механизм узнавания, т. е. должна возрастать величина q.

Обратимся теперь к кинетике отбора. Рассмотрим простой случай — Ai, Di и Qi постоянны и Qi очень близко к единице. Общая организация системы постоянна.

Более сложные случаи также исследованы Эйгеном [43]. Бли­зость Q к 1 позволяет пренебречь членами фцХі в уравнениях (9.14), и последние принимают простую форму

Xi = k0(Wi-E)xi. (9.23)

Интегрирование дает

Xt(f) = xd 0) ехр(^ .

Ехр| k0 ^ Ё(х) dtl

Производя подстановку

N

П хі

Мы увидим, что интегральные члены сокращаются и уравнения (9.23) принимают вид

N

£ xk (0) ехр [k0(Wk~W{)t]

*i = К - К — ^-(0) (9-25)

Это нелинейные уравнения Бернулли типа x + g(t)x + f(t)x? = 0.

Решение (9.25) записывается следующим образом:

Х<(/)==_£іі2(9.26)

Е

Хк (0) Ek tum. n щ ехр (kaWkt)

К-1

При / —► оо сумму экспонент можно заменить наибольшим чле­ном, отвечающим виду с наибольшей селективной ценностью Wm. Этот вид отбирается. Его концентрация стремится к ста­ционарному значению

= (9.27)

Равному п при Qm = 1. Остальные виды исчезают в соответ­ствии с уравнением

Xi{t) = n^j^exp[{Wi-Wm)k0t], (9.28)

Причем некоторые Xi(t) могут проходить через максимум. Пове­дение четырех конкурирующих видов показано на рис. 9.1.

Дарвиновская эволюция трактуется иногда как тавтология — выживание выживающих. Рассмотренная модель показывает,

Однако, что уже в простейшем случае мы имеем дело с выживанием наибо­лее приспособленных к наложенным ограничениям — в данном случае к ус­ловию постоянной организации. Отбор реализуется как процесс оптимиза­ции, наибольшая приспособленность означает максимум селективной цен­ности, т. е. ценности информации при дополнительных ограничениях. Экспо­ненциальный характер решений обес­печивает высокую скорость отбора.

Приведенный расчет является при­ближенным, так как мы пренебрегли членами фцХі, описывающими мута­ции. Как уже сказано, мутации необходимы для эволюции, так как при Qm = 1 система не могла бы развиваться далее. Глав­ная копия «тащит за собой кометный хвост мутантов» [43].

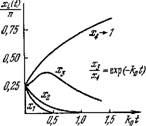
Рис. 9.1. Отбор в системе четырех конкурирующих ви­дов по уравнению (9.26).

1ї', = 1, №, = 4, №3 = 9, №« = 10.

Изложенная теория относится к детерминистическим и, со­ответственно, пользуется дифференциальными уравнениями. В действительности, элементарный процесс, приводящий к по­явлению специфического мутанта, не детерминирован, автока­
талитическое усиление приводит к макроскопическому проявле­нию случайных микроскопических событий. Сам процесс роста численности подвержен статистическим флуктуациям, которые должны учитываться. Эйген провел вероятностное рассмотрение проблемы [43], основываясь на стохастической теории процессов рождения и гибели (см. [45]). Стохастические модели представ­ляют собой в данном случае цепи Маркова [43—46]. Детерми­нистическая теория соответственно модифицируется. Рассмотрим вслед за Эйгеном три примера.

Допустим, что имеется п различных носителей информации, причем каждый из них представлен одной цепью. Редупликация точная, все Qi = 1. Все F{ и Ri одинаковы, т. е. Wi = Е{. Со­гласно детерминистической теории в системе не будет никаких изменений. Стохастическая теория показывает, однако, что си­стема будет утрачивать информацию при распаде каждого неиз­быточного носителя, происходящем до его редупликации. Со­держание информации сузится до немногих или даже одной сильно избыточной последовательности, а затем вся популяция вымрет вследствие «флуктуационной катастрофы». Это неиз­бежно, так как флуктуации образования и распада цепей неза­висимы. Полное вымирание произойдет достаточно быстро — стационарная популяция, состоявшая при t — 0 из п видов, в среднем просуществует в течение времени n/F с t < n2/F. Нет критерия выживания, кроме самого выживания, нет оптимиза­ции.

Если система та же, все Wi одинаковы, но Q, < 1, то судьба всей популяции будет такой же. Однако поведение отдельных носителей информации будет иным. Если Ai — D{ и Qi < 1, то Wi = AiQi — Dj <; 0. Это вымирание компенсируется продукцией новой информации вследствие ошибок копирования. Система «беспорядочно дрейфует в информационном пространстве», но в конце концов уничтожается «флуктуационной катастрофой».

Лишь при Wi Ф Wh и Qi С 1 реализуется устойчивое вос­произведение и отбор цепей с максимальным значением Wm. Пока эти цепи образовались в малом числе, они подвергаются опасности вымирания вследствие флуктуаций. С ростом их числа система становится более устойчивой и, в конце концов, главные копии доминируют в соответствии с детерминистической тео­рией. В этом случае система ведет себя сходно с системой, на­ходящейся в устойчивом равновесии, в котором флуктуации, пропорциональные Vп > несущественны для больших значе­ний п. Однако при образовании системы каждое макросостоя­ние вырастает из микросостояния, представленного вначале единичной копией. Следовательно, для таких метастабильных систем детерминистическое поведение ограничено гораздо силь­нее, чем для систем, близких к истинному равновесию.

Следует остановиться на информационных аспектах описан­ной модели самоорганизации и эволюции информационных мак­ромолекул. Работе Эйгена предшествовала работа Кастлера, имеющая близкое название — «Возникновение биологической организации» [88]. Приведем пространную цитату из этой ра­боты: «В добиологической полинуклеотидной системе почти все последовательности оснований равноправны. Отсюда следует, что такая последовательность сама по себе не имеет никакого «смысла», т. е. не несет никакой информации, являясь лишь «шумом»... Вместе с тем исходная «бессмысленная» последова­тельность становится весьма осмысленной, как только возникает необходимость точно следовать ей. Информация возникла бла­годаря тому, что какая-то одна определенная нить стала праро­дительницей системы, т. е. она возникла благодаря стабильности системы, порожденной этой особой нитью. Следует подчеркнуть, что возникновение информации из шума — это совсем не то, что обнаружение информации, замаскированной шумом, например при выявлении ранее не известной закономерности... Запоми­нание случайного выбора служит механизмом создания инфор­мации, и по своей природе этот механизм совершенно отличен от механизма обнаружения информации».

В свете этих представлений теория Эйгена оперирует не со­зданием новой информации, но обнаружением ранее существо­вавшей, поскольку главная копия закономерно обладает наи­большей селективной ценностью. Отбор идет не по количеству, но по ценности информации.

В моделях, основанных на рассмотрении неустойчивых со­стояний (см. далее, стр. 501, 512), фигурирует уже не выявле­ние ранее существовавшей информации, но ее возникновение в результате случайной флуктуации в начальных условиях.

Вопрос о ценности информации рассмотрен далее (см. стр. 514).