ФИЗИКА ЖИЗНЕННЫХ ПРОЦЕССОВ

ТЕОРИИ МЫШЕЧНОГО СОКРАЩЕНИЯ

Оплатка развил феноменологическую теорию стационарного мышечного сокращения, основанную на неравновесной термоди­намике [68]. Теория исходит из рассмотрения сокращения как пластического течения — движения скользящей модели с тре­нием. Уравнение Хилла (5.19) не выводится из теоретических положений, но используется как опытный факт. Рассматривается скорость химической реакции, скорость расщепления АТФ, | и скорость укорочения V. С помощью уравнения Хилла | связы­вается с нагрузкой Р. Получаемое уравнение имеет вид

I = + + (5.33)

Max max

У разных животных Утах варьирует в 240 раз, /*0 меняется от 0,5 до 4 кГ/см2 (см. [69, 70]). Анализ экспериментальных данных показывает, однако, что сократительная сила /о, развиваемая одним мостиком, примерно постоянна и, следовательно, молеку­лярный процесс, генерирующий эту силу, один и тот же для раз­ных мышц. В теории вычисляется сопряжение химического и ме­ханического потоков [71]. Влияние груза на сродство объясняет­ся тем, что связывание ионов Са++ зависит от изменения длины цепей тропомиозина при изменении нагрузки. В области 0,17Ро < < Р < Р0 сродство растет с грузом — поведение мышечных бел­ков противоположно поведению коллагена, у которого связыва­ние ионов уменьшается с увеличением нагрузки [72]. Связыва­ние ионов Са++ нативными цепями тропомиозина способствует более вытянутому их состоянию. Нагрузка контролирует химиче­ские процессы в мышце посредством регуляторных белков [73]. (Дальнейшие подробности, относящиеся к этой феноменологи­ческой теории, см. в оригинальных работах [68, 74].)

История модельных теорий мышечного сокращения весьма поучительна. В ней отразились различные идеи молекулярной биофизики.

Первоначально, до установления скользящей модели, в ряде теоретических работ исследовалась полиэлектролитная модель (см. стр. 215). Райзман и Кирквуд [75] предположили, что со­кратительным элементом мышцы служит белковая нить, причем некоторые из аминокислотных остатков фосфорилируются за счет АТФ. При этом нить заряжается отрицательно и удлиняет­ся. Таким образом, АТФ ответственна за релаксацию. При рас­щеплении АТФ нить теряет свои заряды и сокращается. Наобо­рот, Моралес и Боттс [76, 77] предположили, что сократительная белковая цепь заряжена положительно (ионы Са++). Благодаря сорбции АТФ эти заряды компенсируются и нить укорачивается.

В мышце действует «энтропийная» упругая сила, подобная силе, определяющей упругость каучука. Предлагались и другие гипо­тезы, основанные на свойствах полиэлектролитов — на свертыва­нии и развертывании белковых цепей, вызываемых изменениями заряда.

Помимо того, что эти теории противоречат ряду описанных выше фактов, учитываемых в скользящей модели, весьма трудно совместить возможные электростатические эффекты в среде, представляющей собой децинормальный солевой раствор, с боль­шими мышечными силами. Р0 составляет, как мы видим, не­сколько кГ/см2 — достаточно вспомнить достижения тяжелоат­летов. Термомеханические свойства мышцы также нельзя объяс­нить в рамках полиэлектролитной модели.

Астбери рассматривал сокращение мышцы как результат конформационного превращения в миозине, возникающего при его взаимодействии с актином [78]. В этой работе не делались какие-либо попытки объединить биохимию и биофизику мышцы, по общая идея, высказанная Астбери, сохранила свое значение.

Френкель предложил трактовать мышечное волокно как ре­зину [79]. Сокращение волокна возникает потому, что увеличи­вается его модуль упругости. Модуль упругости резины тем больше, чем выше степень вулканизации каучука, т. е. чем больше сшивок введено между цепями. Френкель считал, что сшивки в мышце создаются молекулами АТФ.

В работах [80—82] исследовались вязкоупругие свойства по­лимерных материалов. Вязкое течение в таких веществах возни­кает в результате разрыва и образования сшивок под действием теплового движения. Бухталь и Кайзер [54] применили пред­ставления о вязком течении, требующем энергии активации, к мышечному сокращению. Работы [54] и [79] сегодня представ­ляют главным образом исторический интерес, но рассмотрение скользящей модели, основанное на теории внутреннего трения Эйринга, оказывается весьма перспективным (см. § 5.6).

Эйдус считал, что мышечное сокращение вызывается силами поверхностного натяжения в капиллярной системе соприкасаю­щихся миозиновых и актиновых нитей, погруженных в сарко­плазму [83]. АТФ лишь изменяет поверхностное натяжение. В этой работе уже фигурирует скользящая модель, однако ис­ходное предположение о непрерывных контактах между акти­ном и миозином опровергается опытом. Позднее Гамов, видимо, не знакомый с работой Эйдуса, высказал ту же идею, но, в от­личие от Эйдуса, в чисто качественной форме [84].

Другая группа работ опирается на скользящую модель, но предполагает непрерывные электростатические взаимодействия между толстыми и тонкими нитями. В этих работах по существу отвергается мостиковое взаимодействие миозина с актином. Так, в модели Спенсера и Уортингтона [85] возбуждение мышцы оз­начает сообщение нитям актина зарядов, противоположных за­рядам на миозине. Эти заряды перемещаются вдоль нитей ак­тина и функция АТФ сводится к пластификации. Работа [85] не имеет серьезного физического обоснования.

Наличие электростатического дальнодействия между нитями предполагается и в ряде других, более новых работ. Драгомир [86] вводит эти силы для объяснения сохранения объема мышцы при укорочении. В работе [87] рассматривается электрический двойной слой в саркомере. В статье [88] указывается, что элек­тростатические и дисперсионные силы должны быть существен­ны для поддержания «миофибрилльной решетки», но авторы сами приходят к выводу о недостаточности такого объяснения.

Ни в одной из работ этого направления не дано количествен­ное истолкование поведения мышцы.

Следующая группа исследований связана с представлениями о миграции энергии в мышечном сокращении. Сцент-Дьёрдьи, сделавший очень много для биохимии мышцы [89], выдвинул своеобразную гипотезу о природе сокращения [90]. Особо важ­ная роль приписывается воде. Миозин поддерживается в растя­нутом состоянии "специфически растянутой водной структурой. Ее разрушение вызывает укорочение, а восстановление струк­туры— релаксацию. Энергия, необходимая для разрушения вод­ной структуры, подается АТФ. Сцент-Дьёрдьи считал, что бы­строе превращение объясняется миграцией энергии по квазикри­сталлической сетке воды, резонансом энергетических переходов. Его гипотеза спекулятивна — нет никаких доказательств суще­ствования специальной водной структуры в мышце и миграции энергии по этой структуре. Гипотеза Сцент-Дьёрдьи не согласо­вана с результатами электронно-микроскопических и термоме­ханических исследований.

Много позже Мак-Клэйр вновь обратился к рассмотрению ре­зонансного переноса «молекулярной энергии» в мышце [91]. Давыдов предположил, что перенос энергии происходит путем распространения солитона — одиночной, не диссипирующей вол­ны колебательного возбуждения С —О-связей в а-спиралях мио­зина. В результате толстая нить изгибается, обеспечивая перио­дическое замыкание мостиков [92]. Экспериментальных подтвер­ждений эти теории пока не имеют.

Можно думать, что электронно-конформационные взаимо­действия (см. [1], стр. 146) имеют существенное значение в мы­шечном сокращении. Толкающее или тянущее усилие в мышце, где бы оно ни было локализовано, возникает в результате кон - формационного превращения, которое инициируется ионами Са++, т. е. вызывается электронными, зарядовыми, взаимодей­ствиями [93].

Более существенные работы исходят из представлений о фа­зовых переходах в мышце. В 1948 г. Энгельгардт высказал ин­тересную идею о природе сокращения [94]. Предполагается, что в покоящейся мышце белок находится в упорядоченном кри­сталлическом состоянии. Сокращение мышцы происходит в ре­зультате плавления белковых кристаллов. Активной фазой яв­ляется релаксация, а не сокращение. Роль сократительного бел­ка состоит в сопротивлении сжатию, роль АТФ — в воздействии на предполагаемый фазовый переход. Более подробно эта идея была развита Энгельгардтом в работе [95].

Сходная идея была сформулирована Прайором [96]. Выдвигал ее в своих теоретических работах и Т. Хилл [97]. В модифици­рованной форме эти представления сохранили свое значение и в настоящее время. Флори также исследовал мышечное сокраще­ние, исходя из идеи о фазовых переходах [98]. В статьях [99, 100] излагается косвенное экспериментальное подтверждение этих представлений. Авторы цитируемых работ установили, что резкое укорочение под действием АТФ глицеринизированных мы­шечных волокон, погруженных в смеси этиленгликоля и воды, начинается лишь с определенного состава смеси.

Нужно упомянуть, наконец, о попытках скомбинировать на модели относительное скольжение нитей актина и миозина с их свертыванием [101]. Такого рода попытки не привели к убеди­тельным результатам.

После разработки скользящей модели и установления факта мостикового взаимодействия миозина с актином развитие тео­рии мышечного сокращения стало связано, главным образом, с наглядным моделированием этого взаимодействия. Дэвис пред­ложил молекулярное истолкование сокращения [102]. ТММ-вы - ступ может существовать в двух конформациях. В отсутствие ионов Са++ белок находится в неупорядоченной, но вытянутой форме вследствие отталкивания между Mg-АТФ-", присоединен­ным к активному центру, и отрицательными зарядами, располо­женными по соседству. При активации поступивший в сарко­плазму ион Са++ присоединяется к связанной АТФ и образует химическую или хелатную связь с молекулой АДФ, находящей­ся на активном центре актииа. Ионы кальция нейтрализуют заряд АТФ и уничтожают отталкивание. ТММ-выступ испыты­вает конформационное превращение, сокращается и освобож­дает энергию, запасенную в вытянутой коиформации. Такое со­кращение вызывает подтягивание нити актина на один шаг и одновременно переносит присоединенную АТФ в область гипо­тетического активного центра миозиновой АТФ-азы. АТФ рас­щепляется, и мостик, созданный ионом, разрывается. Далее про­цесс повторяется вновь. Количественные оценки параметров со­кращения, следующие из этой модели, не противоречат опыту.

Однако модель встречается с серьезными трудностями. Она не объясняет, каким образом используется энергия АТФ. Непо­нятно, как Са++ образует мостик, если Mg++ уже присоединен к АТФ (см. также [28, 103]).

Тономура и сотрудники предложили мостиковую модель, бо­лее обоснованную биохимически [20, 104]. Схематическое изобра­жение модели приведено на рис. 5.19 и 5.20. Сформулируем ос­новные исходные положения. 1. Сокращение связано с фосфори - лированием и дефосфорилированием миозина. В частности, пря­мой гидролиз фосфорагмиозина активирует миозин. 2. Форма «головки» молекулы миозина изменяется при добавлении АТФ. 3. Связь F-актин — миозин легко расщепляется с образованием комплекса миозин — АТФ при высоких концентрациях АТФ или комплекса миозин — фосфат — АДФ при низких концентрациях АТФ. Прочность связи зависит от конформаций миозина и ком­плекса F-актина с регуляторным белком, конформация которого контролируется следами Са++. 4. Полный цикл происходит вслед­ствие расщепления связи миозин — F-актин после конформа - ционного превращения «головки» миозина, вызванного выделе­нием энергии. Связь восстанавливается, когда молекула мио­зина возвращается в свою исходную форму. Как показано на рис. 5.20, Тономура предполагает различную функциональность S-1A и S-1B частей ТММ.

Наглядные модели Дэвиса и Тономуры требуют детального молекулярного обоснования. Конформационные явления в мыш­це и в мышечных белках изучены пока недостаточно. Установ­лено, что АТФ и АДФ изменяют поглощение света ТММ в обла­сти 280 нм. Конформационное превращение в миозине, индуци­руемое АТФ, следует из опытов по химической модификации миозина, а также из опытов по рассеянию рентгеновых лучей под малыми углами и опытов с флуоресцентными и спиновыми метками (см. [209, 210]). Установлены также конформационные изменения актина [24, 105—109, 211]. Ясно, что конформацион­ные превращения могут быть связаны с фазовыми переходами (см. [110, 111]).

Можно думать, что изложенные выше идеи Энгельгардта, Флори и др. имеют прямое отношение к делу. Выше уже гово­рилось о жидко-кристаллических свойствах сократительных бел­ков (см. стр. 223). Жидко-кристаллическое состояние сократи­тельных фибрилл устойчиво в широком диапазоне условий. В этом диапазоне реализуется полиморфный фазовый переход •типа порядок — порядок. Показано, что структура фибрилляр­ного актина значительно устойчивее, чем структура ансамбля из этих фибрилл. То же относится к тропомиозину. Результаты, полученные на модельных жидко-кристаллических системах, со­гласуются с результатами структурных исследований мышц.

+АТФ

>-ЛДФ

Рис. 5.19. Схема, иллюстрирующая работу мостика.

А —F-актин. ТММ —выступ тяжелого меромиознна, а и 0 — конформацни ТММ. / —посту­пление Са++ и образование мостика, 2— фосфорнлнрование, 3— дефосфорилирование и конформацнонный переход; 4 — разрыв мостика в результате присоединения АДФ и Фн (спонтанный конформацнонный переход).

S-/A у--ф„ S_/B \Са++

І Фн І+АДФ+ФН

Ff ^ г | +атф

5 f+АТФ 3 J

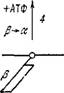
+адф+ф„

+АДФ+4ГК

1

,'МФ Са++ ТММ

Рис. 5.20. Детализированная схема, иллюстрирующая работу мостика. S-ІВ — часть «головки» мнознна, содержащая активный центр АТФ-азы и центр связыва­ния с F-актином, S-IA содержит только цеитр свявання с F-актином. / — поступление Са + +, связывание S-IB, 2 — фосфорнлнрование, 3— дефосфорилирование, конформацнонный пере­ход, скольжение, 4 —связывание S-IA, 5—образование комплекса миозина с АДФ н Ф в —диссоциация связи S-ІВ, спонтанный конформацнонный переход. 7 — обмен связи S-IA S-ІВ, в— разрыв мостика.

В процессе укорочения мышцы меняется период решетки, по­строенной из протофибрилл. При вдвижеиии решетки тонких ни­тей в решетку толстых нитей тетрагональная симметрия заме­няется гексагональной, т. е. решетка тонких нитей претерпевает полиморфный переход [106—109].

Дальнейшее изучение этих явлений весьма актуально. Мы еще не располагаем убедительной молекулярной картиной мы­шечного сокращения. Другие конкретные модели поведения мо­стика миозин — актин предложены в работах [112—114].

Первая попытка построить количественную физическую тео­рию, основанную на мостиковой — скользящей модели, принад­лежит А. Хаксли [115]. Предполагается, что активный выступ ТММ (обозначаемый далее М) осциллирует на некотором про­тяжении вдоль тонкой нити, а активный центр актина А фикси­рован неподвижно. Реакции имеют вид

А + М->АМ (Образование мостика), АМ+ АТФ-* А - АТФ + М (Разрыв мостика), А • АТФ -> А + АДФ + Фн (Расщепление АТФ).

Константам скоростей двух первых реакций приписываются " определенные зависимости от расстояния между А и М вдоль миофнбриллы. Решение учитывает относительное перемещение А и М при укорочении саркомера.

При надлежащем подборе нескольких параметров Хаксли получил численное согласие механических характеристик мыш­цы с результатами их вычисления по уравнению Хилла (см. также [116]).

(5.34)

(5.35)

H = ki («о — п — т) — п т — тіі — k2m.

Здесь vjL — константа скорости превращения тянущих мостиков в тормозящие, равная скорости относительного перемещения ни-

Теория А. Хаксли была упрощена и усовершенствована Де- щеревским [117]. В его работе рассматриваются три состояния мостиков: замкнутые мостики, развивающие тянущую силу, зам­кнутые мостики, тормозящие скольжение нитей, и разомкнутые мостики. Мостики замыкаются независимо друг от друга и тя­нут нити, вызывая активное сокращение; далее те же мостики тормозят движение, так как нити переместились, и, наконец, мостики разрываются. Обозначив через «0 полное число актив­ных ТММ-выступов в половине толстой нити, через п — число тянущих и через т — число тормозящих мостиков, можно напи­сать следующие кинетические уравнения:

Тей v, деленной на расстояние L между двумя соседними актив­ными центрами актина, на которых может быть замкнут мостик. К этим уравнениям добавляется выражение второго закона Ньютона

Mb = fQ(n — т) — fn0, (5.36)

Где М — перемещаемая масса, /0 — сила, развиваемая одним тя­нущим мостиком, f — внешняя сила (нагрузка), приходящаяся на один мостик. В сущности, уравнение (5.36) описывает движе­ние с трением (ср. стр. 247), выраженным как fQm. В стационар­ных условиях п = rh — 0 и сі = 0. Исключая из (5.34) — (5.36) п, т и «о, находим для стационарного состояния

{f + a)v = b(f0-f). (5.37)

Это уравнение совпадает с характеристическим уравнением Хилла (5.19). Все величины в (5.37) отнесены к одному мостику, v — скорость укорочения в половине саркомера. Константы а и b выражаются через ku k2, f0 и L следующим образом:

A—kЇТЇГЛь (5.38)

Ь = т№ъ-ак>Ь (5-39>

Итак, эмпирическое уравнение Хилла выведено теоретически на основе модельных представлений. Этот вывод показывает, что уравнение Хилла отвечает стационарному скольжению нитей с силой трения, пропорциональной скорости. В самом деле, если rh — 0, то из (5.35) следует

И второй закон Ньютона перепишется в виде

Ми = fori — v — fn0. (5.40)

Дещеревский впервые вывел теоретически уравнение Хилла. Мы видим, что цикл Дещеревского ие включает обратных про­цессов. При их учете получаем (см. стр. 61)

&[/г2-£-= k-1k-2k-3,

И если k-i, k-2 - С ku k2, то /г_3 » vjL.

Должен быть, следовательно, второй цикл, приводящий в движение цикл Дещеревского. Этот второй цикл — замкнутая цепь химических превращений, в ходе которых расщепляется АТФ. Теория Дещеревского дает правильное стационарное решение для изотонического сокращения. Однако она не объяс­няет развитие напряжения при изометрическом сокращении.

Подробный анализ теории А. Хаксли содержится в ра­боте [118].

Т. Хилл, исходя из ранее развитой им теории фазовых пере­ходов в линейных регуляторных системах [119], предложил рас­сматривать сокращение саркомера как фазовый переход первого рода между двумя состояниями белковых нитей — без мостиков и с мостиками [97]. Первому состоянию соответствует растянутый саркомер, в котором нити миозина и актина не перекрываются, второму — укороченный с перекрытием нитей. Приложенная на­грузка препятствует фазовому переходу, условие которого можно записать в виде

F0L — AG. (5.41)

Химизм процесса не учитывается, роль АТФ сводится к неболь­шому изменению AG. Позднее Т. Хилл отказался от этой теории, главным образом потому, что сила Ро не постоянна, но зависит от длины саркомера (см. стр. 230) [120]. Очевидно, что теория мышечного сокращения не может быть построена в рамках рав­новесной термодинамики. Речь идет о кинетических процессах. Дальнейшие работы Т. Хилла и сотрудников посвящены усовер­шенствованию теории Хаксли [121, 122]. Однако рассмотрение в них не удалось провести в такой простой и ясной форме, как в работе Дещеревского.

В работе [210] дан обзор ряда альтернативных скользящих моделей.

Теория нестационарного кинетического поведения мышцы развита также в работах [114, 117, 123, 134, 139, 211, 212]. К этим вопросам мы вернемся в § 5.10.