ФИЗИКА ЖИЗНЕННЫХ ПРОЦЕССОВ

ПЕРИОДИЧЕСКИЕ ЯВЛЕНИЯ В МЕМБРАНАХ

Мембраны клеток и внутриклеточных органоидов в значи­тельной степени определяют их свойства. Естественно думать, что и периодические процессы, присущие живым организмам, связаны с периодическими явлениями в мембранах.

Нелинейное поведение возбудимых мембран отчетливо про­является в генерации и распространении электрического им­пульса (см. гл. 5). Здесь мы рассмотрим периодические измене­ния состояния мембран, наблюдавшиеся в ряде опытов (см. [88]). Теорелл показал, что в условиях взаи­модействия ионного и объемного потоков через мембрану возможно ее нестацио­нарное поведение вследствие периодиче­ского изменения ионной проводимости

. Теория этих явлений рассмотрена далее. Шашуа наблюдал колебания элек­трического потенциала в очень тонких двойных полиэлектролитных мембранах

IMF

М

А Штр. ft

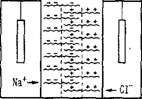
Рис. 8.36. Схема трех­слойной полиэлектролит­ной мембраны.

. Двойной слой состоял из поликис­лоты (а) и полиоснования (Р). Таким образом, в нем имелись три зоны — от­рицательно заряженная а, нейтральная и положительно заряженная р (рис. 8.36). Мембрана помещалась между двумя оди­наковыми растворами 0,15 М NaCl. При наложении отрицательного потенциала со стороны полиоснования (+) наблю­дались периодические спайки и при некотором критическом зна­чении тока — незатухающие колебания, сохранявшиеся часами. Ток через мембрану состоит из перемещения катионов сквозь зону а и анионов сквозь зону р. В результате в центральной нейтральной зоне накапливается NaCl. Возрастание осмотиче­ского давления приводит к появлению потока растворителя в мембрану и возрастанию в ней гидростатического давления. С другой стороны, увеличение концентрации соли вызывает сокращение молекул полиэлектролита, что также увеличи­вает гидростатическое давление. Когда это увеличение пре­взойдет увеличение осмотического давления, поток растворителя изменит знак, и концентрация соли в мембране увеличится еще больше. Возникает концентрационный градиент, соль покидает мембрану и продолжает вытекать после того, как Мембрана достигнет максимального сокращения. Затем насту­пает релаксация, возвращение мембраны в исходное состоя­ние, и процесс начинается сначала. Теоретическое рассмо­трение этого автоколебательного процесса, поддерживаемого

Постоянной внешней силой, проведено Качальским и Спангле- ром [88].

Мембранный осциллятор Теорелла [89] состоит из двух ячеек, заполненных электролитом разной концентрации и раз­деленных мембраной из пористого стекла, содержащей связан­ные отрицательные заряды. При пропускании постоянного тока создается разность потенциалов на двух сторонах мембраны, и в ячейках возникает сдвиг уровней жидкостей. При сильных по­стоянных токах в системе происходят периодические колебания уровней жидкостей и мембранного потенциала, разнящиеся по фазе. Это — электрокинетическое явление. Вследствие того, что мембрана содержит фиксированные отрицательные заряды, электролит в ее порах несет преимущественно катионы. Внеш­ние поля заставляют перемещаться катионы и растворитель. Распределение концентраций в порах мембраны зависит от ко­личества протекающей жидкости и скорости ее течения, от чего зависит и сопротивление мембраны.

Допустим, что концентрация элек­тролита в левой ячейке выше, чем в правой. Пропустим через мембрану ток, направленный справа налево. Возникнет следующая качественная картина [91]: поток воды, направлен­ный справа налево, заставит разбав­ленный раствор NaCl войти в мем­брану, где возникнет вогнутый про­филь концентрации (рис. 8.37). Со­противление мембраны становится больше сопротивления покоя, соответствующего прямолиней­ному профилю концентрации. Падение потенциала на мембране начнет расти, что в свою очередь приведет к увеличению сопро­тивления и к росту мембранного потенциала. При достаточно высоком гидростатическом давлении скорость потока уменьшит­ся и вогнутый профиль концентрации вернется к первоначаль­ной прямолинейной форме. При этом возникнет избыток гидро­статического давления над осмотическим, и водный поток нач­нет двигаться в обратном направлении. Поток действует на концентрационные профили как искажающий фактор, а диф­фузия— как фактор восстановления.

Скорость течения жидкости через мембрану выражается фор­мулой

Ы = а Ар — р Ai|), (8.109)

И>0

"І

Рис. 8.37. Распределение кон­центраций электролита в мембране в зависимости от направления потока.

Где Ар — разность гидростатических давлений, а, (3 — коэффи­циенты. При не слишком малых значениях \и\^> D/d, где с?—

Толщина мембраны, D — коэффициент диффузии, болыцая часть ее заполнена электролитом одной и той же концентрации с, или с2 в зависимости от направления скорости. Соответственно вольт-амперная характеристика состоит из двух линейных участ­ков с резким переходом между ними (рис. 8.38). Наклоны пря­мых определяются сопротивлением, а переход между ними про­исходит при разности потенциалов фо, соответствующей и = 0. Возникновение колебаний связано с на­личием падающего участка зависимости 1 і( ф). В некоторых пределах каждому значению тока соответствуют три значе­ния разности потенциалов фь ф*, фг. Зна­чение ф* отвечает неустойчивому состоя­нию, фь ф2 — устойчивым. В процессе ко­лебаний между ними происходят пере­ходы [92].

Теория колебаний мембранного ос­циллятора развита Теореллом [89, 91], японскими авторами [92] и Франком [93]. В работах Маркина и сотрудников [94] построена теория распространения возбуждения в системе Тео­релла. Волна возбуждения возникает в связи с переходом мемб­раны из одного устойчивого состояния в другое. Показано, что переход возможен только в одном направлении, зависящем от величины поляризующего тока. Рассчитана скорость распро­странения волны как функция поляризующего тока в согласии с опытом.

Таким образом, в мембранных системах вследствие нелиней­ности могут возникать явления гистерезиса и связанные с ними периодические процессы. В биологических мембранах, содержа­щих белки — ферменты, обладающие кооперативными свойст­вами, периодические изменения состояния мембраны могут оп­ределяться нелинейной связью между диффузией и химическими реакциями. Рассмотрим, следуя работе [88], некоторые простые примеры.

Допустим, что фермент катализирует необратимый распад субстрата S

JX„M = -^=KES, (8.110)

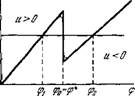
Рис. 8.38. Вольт-ампер­ная характеристика си­стемы Теорелла.

Где S — концентрация субстрата, К — константа скорости, Е — концентрация фермента. Пусть имеется критическая концентра­ция субстрата So, при которой фермент испытывает кооператив­ное конформациониое изменение, приводящее к повышению его активности. Константа скорости К изменяется от до К.2- За­висимость /Хим(5) показана на рис. 8.39. Субстрат поступает
в систему посредством диффузии через мембрану, идущей со скоростью

^ = (8.111)

Где Se — концентрация S в источнике, которая считается прак­тически ПОСТОЯННОЙ (Se = const). При /хим = / диф, S = = — Sxiim + 5дИф = 0 и система находится в стационарном со­стоянии. Рис. 8.39 показывает различие между двумя стацио­нарными состояниями, отве­чающими Se = S'e (а) и Se= = S" (b). Точка пересече­ния а кривой /хим и прямой /дИф устойчива, так как при малом положительном из­менении 5 /хим>/'диф и концентрация субстрата убывает, пока система не вернется в точку а. С дру­гой стороны, при отрица­тельной флуктуации /дИф > > /хим и концентрация суб­страта возрастает, пока си­стема вновь не вернется в точку а. Напротив, если точка пересечения b графи - А0В ^хим и ^диф лежит в области неустойчивости, положитель­ной флуктуации 6S отвечает > /хим и концентрация возрас­тает вплоть до точки с. В этой точке фермент испытывает кон - формационное превращение, и система переходит в точку d, в которой /хим > /дИф. Концентрация S убывает до точки е, в которой фермент испытывает обратный переход в исходную форму, система переходит в точку f. Здесь концентрация воз­растает вновь, так как /" > / „, и система вновь достигает

ДИф хим

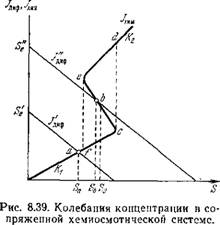
Точки с. Таким образом, система выходит на цикл гистерезиса cdef, которому отвечает предельный цикл на фазовом портрете.

Второй пример — продукция некоторого вещества Q с по­стоянной скоростью. Когда Q достигает критического зна­чения Q0, фермент испытывает конформационное превращение и скорость продукции Q падает до /®м. Реакционное простран­ство соединено с внешним резервуаром через мембрану, и Q подается со скоростью

(8.112)

Так что

Q = /xhm — /диф - (8.113)

В этом случае также возникают гистерезисная петля и коле­бания.

Третий пример, рассмотренный Качальским и Спанглером [88], — постоянный ферментативный процесс, сопряженный с ко­оперативным изменением проницаемости мембраны от до а2 при некотором значении концентрации продукта Q (рис. 8.40). Если мембрана разделяет два раствора соли одинаковой концентрации и реак­ция в мембране сама продуцирует ионы, то концентрация соли внутри мембраны отличается от ее концентрации во внеш­ней среде. Возникает разность потенциа­лов, которая испытывает колебания, если внутримембранный процесс кооперати - вен.

Как показывают эти примеры, коопе­ративные свойства мембран могут быть причиной незатухающих колебаний, что естественно, так как кооперативность всегда означает нелинейность. Эти явле­ния изучены, главным образом, на экс­периментальных и теоретических моде­лях. Пока отсутствуют детальные исследования, раскрывающие молекулярные механизмы мембранных процессов, ответствен­ных за биологические ритмы. Однако общие подходы к таким проблемам развиты, и периодические процессы в клетках нельзя более считать загадочными.

Обсуждаемые явления можно феноменологически описать на языке нелинейной термодинамики [88]. Задачи дальнейших ис­следований достаточно трудны, так как их решение требует де­тального изучения молекулярной структуры и динамики биоло­гических мембран.