ФИЗИКА ЖИЗНЕННЫХ ПРОЦЕССОВ

АВТОКОЛЕБАНИЯ В ФЕРМЕНТАТИВНЫХ РЕАКЦИЯХ

Нелинейности в кинетике биохимических, ферментативных, процессов проявляются в ряде случаев в наблюдаемой их перио­дичности. Происхождение колебаний в биохимических системах в целом понятно — они определяются автокаталитической си­стемой реакций и в этом общем смысле моделируются периоди­ческими реакциями в неживой природе. Таковы процессы, изу­ченные Жаботинским и описанные в § 8.5, периодические окис­лительные реакции, теория которых развита Франк-Каменецким [65], и т. д. Общие обзоры, посвященные биохимическим коле­баниям, содержатся в сборнике [66] (см. также статью Селькова [67] и монографию Жаботинского [19]).

Особенно четко периодичность биохимических процессов про­является в реакциях гликолиза (анаэробного превращения ше - стичленных Сахаров в трикарбоновые кислоты), сопровождаю­щегося синтезом АТФ [68, 69]. Упрощенная схема процесса по­казана на рис. 8.29 [68]. В опытах Чанса, Гесса и сотрудников были обнаружены сначала затухающие концентрационные коле­бания в гликолизе [70—72], затем были найдены условия воз­никновения незатухающих автоколебаний [73—75]. На рис. 8.30 показаны колебания концентрации одного из продуктов реакции гликолиза — НАД-Н [73], примечательные своим почти сину­соидальным характером.

Реакция гликолиза реализуется в сложной полифермент­ной системе. Возможности возникновения автоколебаний в таких системах были исследованы Сельковым ([67, 76 -82], см. также [19]).

Проведем рассмотрение этой проблемы, следуя работе [79]. Химические процессы, подчиняющиеся закону действия масс, как правило, нелинейны. Нелинейны взаимодействия элементов полиферментной системы и взаимодействия таких систем друг с другом. В результате возникают регуляторные системы, так как их устойчивость непосредственно связана с нелинейностью. Сельков выделяет ключевые этапы в полиферментной системе, характеризуемые наиболее сильной нелинейностью и ответствен­ные за регуляцию процеса. Эта основная нелинейность прояв­ляется в гистерезисной зависимости квазистационарной скорости

Ключевой реакции от концентрации субстрата. Основная нели­нейность возникает в результате совокупности механизмов, дей­ствующих независимо друг от друга.

Примером типичного био - J

Химического нелинейного про­цесса служат ферментативные реакции, ингибируемые избыт­ком субстрата или кофермен - та, например, реакции с уча­стием биосинтетических дегид - рогеназ, ингибируемые НАДФ - Н+. Такую реакцию можно представить схемой, показан­ной на рис. 8.31. Реакция

АТФ

К

-АДФ Сз Глюнозо-В-фосфат

L-—АТФ | АДФ

С3 Фрутш-1,0-&1ф№фт

Дио/гси - ацетт - фасфат

Л3

Ч

<?С3 Глщеролг>0ееа(?-3-фосфат

X + Y' —» X' + Y,

Катализируемая ферментом Е, ингибируется активной фор­мой кофермента Y'. Скорость v конверсии Х->Х' в стацио­нарных условиях можно выра­зить приближенной формулой

= УХУ'

° К, [к2 + У {1 + (Y'IKi)y}] '

(8.89)

Где V — величина, имеющая размерность скорости, пропор­циональная концентрации фер­мента. Скорость поступления субстрата vu скорость регене­рации кофермента из неактив­ной формы v2 и скорость ис­пользования кофермента Уз представим формулами

(8.90)

V\ = vm — k, X,

Щ = k2Y,

= W;

Щ, Фн НАД-Н

<?С5 1,3-

4с'ЛДФ

I f—ТФ

Л3 3-

(I

2Zi г-

Tl

£Сз фасфажллируеат — /АДФ

-^/АТФ

НАД

/Cj Дарует — НАД-Н

НАД-Н ч ■ НАДО/

Дахтат Ртатл (мышца) (фажжц)

Рис,

8.29. Упрощенная схема гли­колиза.

3

Св, С) — шести - и трехуглеродные соедине­ния, 1—4— реакции, определяющие кине­тику процесса в це. том.

Здесь X, У, У — концентрации, vm — максимальная скорость реакции X X', Ки К2, Кі — константы, у — порядок ингибиро - вания фермента коферментом Y'. У + Y' = У0 — постоянная ве­личина и имеется большой избыток X и Y', т. е. Х/Е, Y'/E » 1.

Введем безразмерные переменные vx_ , _ г_

KiK 1 V

V

Уо*

УУо

(8.91)

Б=

Р=

E =

V =

" Уо ' [5] А.

* _ V0Kx ' у

JU

K2 + k3 ' Vm

Ко '

Vm = •

Ay

(8.92)

■ v, — v,

У — V,

Y „ '

V0 = (k2+k3)Y, n

Vi = y

* 0

Кинетические уравнения имеют вид dx dx

Vt ( Кг У

КГ' а = (т7І'

Где

Хг/

V =

Vl=vm — px.

Квазистационарная скорость реакции v определяется из урав­нения

V = T-T7#—тт^Г. (8.93)

I + у' (1 + at/y)

Где у' = б — v — квазистационарная концентрация кофермента.

0,5

1,5

2,0 2,5 t, vee:

Рис. 8.30. Колебания концентрации НАД-Н в экстракте дрожжей.

1,0

О

Из этих значений v и у' находим концентрацию субстрата

* = v + 1 + а (б - v)v) . (8.94)

, vz V'±==Y

Реакция с субстратным сливаются, образуя^ точку пере-

Выходные характеристики системы, т. е. значения х, нахо­дятся из уравнения (8.94) путем подстановки значений v, удо­влетворяющих условию 0 < х < < б. Область существования S - образной нелинейности ограни­чена значениями параметров,

Скачкообразные переходы между стационарными состояниями (ср. [7]). Возникает также возможность генерации импульса реакции в ответ на надпороговое возмущение параметров. На­конец, возможны автоколебательные состояния. На рис. 8.32 показаны три стационарных состояния, отвечающих пересече­нию S-образной входной характеристики v(a:) с прямой vj = = vm — Р*- На рис. 8.33 показаны устойчивый и неустойчивый предельные циклы, окружающие неустойчивые стационарные состояния.

Юг

У(х)

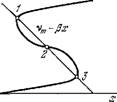
Рис. 8.32. Несколько ста­ционарных состояний, возникающих вследствие нелинейности входной характеристики.

Сельков отмечает, что распространенное мнение о малых временных постоянных автоколебательных биохимических про­цессов ошибочно. Периоды колебаний порядка суток и больше возможны, например, если субстрат X может обратимо перехо­дить в неактивную форму [81]. Соответствующий расчет приве­ден в [79].

Можно показать, что существует неограниченное разнообра­зие биохимических механизмов, подобных рассмотренной реак­ции и, тем самым, обладающих такой же нелинейностью. Такие модели рассмотрены в [79] (см. также [19]). Различные меха­низмы могут взаимодействовать друг с другом. Нелинейные си­стемы являются регуляторными. Факторы, прямо или косвенно влияющие на стационарные состояния или воздействующие на основные нелинейности биохимических реакций, определяют их динамическое поведение. Даже малое изменение поступления субстрата может, например, привести к исчезновению автоколе­бательного режима и к исчезновению альтернативных стацио­нарных состояний. Таким образом, основная нелинейность под­лежит строгому контролю.

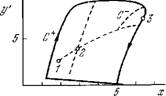
Рис. 8.33. Устойчивый (С+) и неустойчивый (С~) предельные циклы.

1, 2, 3— стационарные состояния. а=100, 13 = 0,08, 7 = 3,6 = 0,9, £ = 0,01, vm = 0,825.

K2 к + у ■ j

Реакция гликолиза является ярким примером нелинейного биохимического процесса. Рассмотрим ее подробно, следуя за изложением в [18], основанным на работах Селькова (в част­ности, [82]) и Хиггинса [63]. Обратимся к схеме, показанной на рис. 8.29. Кинетика процесса в целом определяется несколькими «узкими местами», обозначенными на схеме цифрами. Обозна­чим через у0 скорость реакции 1, катализируемой ферментом гексокиназой (ГК). Реакция Cg+riCg' быстрая и обратимая, поэтому будем считать, что концентрации этих веществ пропор­циональны друг другу— устанавливается квазиравновесие. Кон­центрация X одного из веществ Cg, С" возрастает со скоростью 1>о и убывает за счет реакции 2, катализируемой фосфофрукто - киназой (ФФК). Далее, вплоть до реакции 3, протекает не­сколько быстрых обратимых реакций и, следовательно, концен­трации промежуточных веществ пропорциональны друг другу. Обозначим одну из этих концентраций через У. ФФК активи­руется продуктами своей реакции, т. е. веществом Y. Поэтому увеличение У за счет реакции 2 зависит как от X, так и от У. Скорость возрастания У равна скорости убыли X. В реакции 3, катализируемой пируваткиназой (ПК), У убывает. Получаем ки­нетические уравнения [63]

(8.95)

В работе Селькова [82] вместо множителя Y/(Ky-\- У) фигури­рует Y2/(Ky Y2), т. е. вводится более высокий порядок акти­вации ФФК, что обосновывается биохимически. Однако уже простая система (8.95) характеризуется интересующей нас не­линейностью, и результаты расчетов в работах [63] и [82] сходны друг с другом. Более того, автоколебательный режим полу­чается и при дальнейшем упрощении, если принять, что Кх ^ X, Ky ^ Y. Получаем систему

(8.96)

Подобную системе Лотка (см. стр. 440). Здесь k[ = kyIKxKY, = k2/K. Очевидно, что Do пропорционально содержанию ГК, k[ — содержанию ФФК и ^—содержанию ПК- Стационарные концентрации X и У равны

Введем безразмерные переменные

V./k

Тогда (8.96) примет вид

Dx.

(8.97)

*Г=1-ХУ>

Dx аУ{х і +гу)'

Где

V*

V0 /К

Фазовый портрет системы на плоскости х, у и главные изоклины показаны на рис. 8.34. Изоклина вертикальных касательных (/) — гипербола у = х~\ горизонталь­ных касательных (//) — гипербола л; = (1 + г)/(1 + гу) и прямая у — 0. Линеаризуя уравнения (8.97), опреде­ляем характер особой точки О. Корни характеристического уравнения равны

Voki

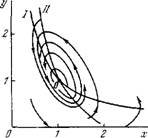
Рис. 8.34. Фазовый портрет колебаний при гликолизе. i, ii — изоклины.

1 + МО-

\2 4а 1'/»

Г) 1 +г J '

1 4-і

При 4а/(1 + г)>(1 — ar/( 1 + г))2 точка О есть фокус. Если аг/(\ + г)<0, фокус устойчив, если аг/(1 + г) > 0, фокус неустойчив и вокруг него воз­никает предельный цикл. При arl( \ + г) = 1 происходит бифур­кация. Вблизи этой точки, если \аг/(\-\-г)—1|<С1, частота колебаний равна мнимой части корня характеристического уравнения, т. е.

V-

(0 :

1 +Г

(8.98)

Таким образом, при определенных условиях система (8.96) дей­ствительно дает автоколебания. Увеличение параметра а спо­собствует их нарастанию, уменьшение а — затуханию. Из вы­ражения для а следует, что уменьшение k[ и скорости притока £>о должно вызывать самовозбуждение колебаний. К тому же результату должно приводить увеличение^, т: е. добавка ПК. Это согласуется с опытом.