ДВИЖЕНИЕ ЖИДКОСТЕИ И ГАЗОВ В ПРИРОДНЫХ ПЛАСТАХ
Качественные методы теории напорных течений
Эффективные решения, подобные приведенным в предыдущем параграфе, можно получить лишь для фильтрационных течений в сравнительно простых областях. В других случаях расчет полей течения связан с большими трудностями. Заметим, однако, что в прикладных задачах представляют интерес не столько сами поля, сколько некоторые их интегральные характеристики, чаще всего дебиты при заданных перепадах давления. В теории напорной фильтрации можно установить несколько основных принципов, которые позволяют получать оценки для дебитов в областях сложной формы без вычислений. Изложим некоторые из этих принципов и продемонстрируем на примерах, как ими можно практически пользоваться.
Основная задача теории пространственных напорных стационарных течений состоит в отыскании поля давлений р(х) в некоторой пространственной области D, внутри которой задано поле проницаемости k (х), а на границе С области D задано либо давление р, либо нормальная составляющая скорости фильтрации ип (поток жидкости). Будем считать, что на части границы Ср задано давление, а на С, — поток:
Р! ср = Р (*), un! Cq = — k (dp/dn)/Cq = q(x). (11.37)
Здесь P (x), q(x) — заданные функции. Внутри области D давление и скорость фильтрации удовлетворяют, как было показано выше, системе уравнений ':
V» = 0, и = — (k/\i) ур, (11.38)
Откуда можно получить уравнение для давления
V (kyp) = 0. (11.39)
Вариационные принципы. Рассмотрим интеграл по области D
A=$(vw)dV, (11.40)
D
Где v и <р — произвольные векторное и скалярное поля, обладающие достаточной гладкостью. Если векторное поле v солено- идальное, т. е. удовлетворяет условию уг» = 0, то, используя формулу Остроградского — Гаусса, получим
А = J MdS — l^vdV = f VnfdS. (11.41)
CDC
В частности, подставляя p вместо у и и вместо v, получим
А — §(uyp)dV = IpUndS. (11.42)
D С
Здесь [pundS — работа, совершаемая в единицу времени внеш»
С
Ними силами давления, на вдавливание жидкости внутрь выделенного объема.
Подынтегральное выражение в левой части уравнения (11.42) характеризует энергию, затрачиваемую на работу жидкости в единице объема среды на преодоление сил трения, и потому представляет собой плотность диссипации энергии — количество энергии, переходящее в тепло в единице объема пористой среды. В целом соотношение (11.42) выражает собой тождества полной диссипации: вся работа внешних сил над жидкостью в элементе пористой среды переходит в тепло. Это тождество верно для произвольного фильтрационного течения несжимаемой жидкости и для стационарных течений сжимаемой жидкости.
Определим для векторного поля и и скалярного поля р положительные функционалы X и Y:
X = Г = і W-'IVPI2^. (II.43)
2 D r 2 D
Можно установить следующие утверждения.
1. Из всех соленоидальных векторных полей v, удовлетворяющих в точках части границы Cq условию
Vn\c9 = g, (11.44)
Решение и («истинное поле скоростей фильтрации») выделяется тем, что минимизирует функционал
Х*[©]= X[tr] + J/tK>„rfS, (11.45)
Ср
Называемый полным потенциалом диссипации.
2. Из всех скалярных полей <р, удовлетворяющих условию на Ср
? \ср = Р, (11.46)
Решение р («истинное поле давлений») выделяется тем, что минимизирует функционал
У* [?] = Пт] + (П.47)
Ся
Называемый полным дополнительным потенциалом диссипации.
Докажем первое из этих утверждений. Пусть и — решение, а v — пр оизвольное поле, удовлетворяющее граничному условию (11.44) и условию соленоидальности. Тогда
X* [©] - X* [и] = ± Uф) (v2 - и2) dV — j р (vn - un)dS =
TOC \o "1-3" \h \z ~ D Ср
= 11 (ц/Л) — я) (v + u)dV — J р {v — и) ndS > 2 ср
> f (p./k) (v — u)udV — [p(v — u)ndS —
D Cp
= —l(v — u)T}pdV — ]p(v — u)ndS. (11.48)
X* [г>] — X*[u\>[p{v — и) ndS —
С
— $p(v — и) ndS = (V — и) ndS = 0. (11.49)
С„ са
Тем самым мы показали, что истинное поле скоростей и минимизирует полный потенциал диссипации X* [о]. Точно так же доказывается, что истинное поле давлений р минимизирует полный дополнительный потенциал диссипации F* [?].
Следствия из вариационных принципов. Сформулированные вариационные принципы можно использовать для построения решений прямыми вариационными методами. Здесь же рассмотрено применение этих принципов для качественного исследования и построения оценок решений.
|
(11.50) |
Прежде всего можно установить единственность решения задачи: допустив существование двух различных решений системы (11.38) при условиях (11.37), получим противоречивые неравенства
X* Ш > X* Ш, X*lui}<Xluth
Откуда следует, что X* [иі] = X [вг]. Но в силу рассуждений, подобных (ІІ.48),
X [и,] — X [»2] = \ \jvlk) («і - u2fdV. (11.51)
Таким образом ui = »2 — решения совпадают.
|
Используя тождество (11.42), получим из (11.48): |
Далее для давления справедлив принцип максимума: давление принимает свои наибольшее и наименьшее значения на границе области. Действительно, допустим, что в области D максимум давления Р* больше, чем на границе Р+. Следовательно, максимальное давление достигается во внутренней точке области М*. Тогда найдется внутренняя подобласть De области D, содержащая точку М*, на границе которой р — Р* — е. Рассматривая решение уравнения (11.39) в подобласти DE и учитывая его единственность, найдем, что давление Р постоянно по всей подобласти Dt: р = = Р* — г < Р*. Это противоречит условию, что р(М) = Р*. Полученное противоречие и доказывает принцип максимума.
|
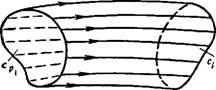
РИС. 4. Укрупненная трубка тока
|
|
Сч ч |
|
'2 Ограничимся в дальнейшем наиболее существенным для |
Из нашего рассуждения следует еще одно важное утверждение: поверхности постоянного давления (изобары) в стационар-
Ном фильтрационном потоке либо заканчиваются и начинаются в точках границы, либо — если они замкнуты — содержат внутри участок границы области (такое может быть только в том случае, если область движения многосвязна).
Практики случаем, когда область фильтрации представляет собой укрупненную трубку тока (рис. 4), т. е. ограничена непроницаемой боковой поверхностью Cq, на которой ы„ = 0, и двумя поверхностями постоянного давления Сі и С2 (вход и выход), на которых давление принимает значения Р{ и Р2, Р\>Р2 соответственно. Большинство задач, связанных с расчетом дебитов скважин и суммарных объемов отбора по месторождениям, принадлежит именно к этому классу. Разность Р = Р\ — Р2 будем называть перепадом давления на данной трубке тока, а полный поток жидкости через произвольное сечение трубки тока — расходом:
Q = — S undS = У undS. (И.52)
С, Сг
Чаще всего нас интересует именно расходная характеристика фильтрационного потока — зависимость Q(P)— или, поскольку она, очевидно, линейна — коэффициент расхода
Л = Q/P = const. (11.53)
Допустим, что найдено решение задачи теории фильтрации, т. е. поля и и р для трубки тока. Тогда имеем соотношения
У* \р] = ^ Ш (Vp)2dV = ±$UVxpdV =
= - UunpdV = UPi-P2)Q; (11.54)
* dD z
A = P~2J (%)|v/>|W. (11.55)
D
Далее, поскольку функции и, p — решение задачи теории фильтрации, имеем
X* [»] =41Ш u4V + JpUndS =*S(uw)dV-
Cp LD
— (Pi — я2) Q = — і. (Pi ~Pi)QL = \ Q2/Л = -4 u2dV,
(11.56)
Так что A = —~Q2/X*[u]. (11.57)
Соотношения (11.55) и (11.57) можно многими способами использовать для получения оценок коэффициента расхода, продуктивности Л и доказательства общих утверждений относительно зависимости других величин от геометрических и физических параметров пласта.
Действительно, возьмем произвольное скалярное поле ср, удовлетворяющее условиям tp|Cj=l, ср |с, = 0, и произвольное солено- идальное векторное поле v. Тогда в силу доказанных вариационных принципов
А = (цР2)-1 J k | Vp IW = r-11f k І у (Р/Р) I2 dV =
D D
= p-1minJyfe|v?|W<[A-1U|vf 12dV. (11.58)
Таким образом, из (11.55) следует неравенство (11.58) — оценка сверху для коэффициента продуктивности. С другой стороны, из вывода принципа минимума потенциала диссипации X* следует, что, если рассматривать не все поля скорости, а только поля, отвечающие фиксированному расходу Q, то на них решение также минимизирует функционал X* и, следовательно,
X* [и] = ^ H~lu4V — QP< І (і Sk-WdV - QP, (И-59)
2D 2 D
Рассмотрим «нормированное» поле
«о = u/Q. (11.60)
Очевидно, этому полю будет соответствовать единичный расход, Q[«o]= 1, и в силу линейности задачи оно будет минимизировать интеграл
L$k-lvodV (11.61)
2 D
На всех соленоидальных векторных полях vo с единичным расходом. Теперь имеем:
А = — jQ2/X* [и] = j*-1Q2/= ц-'/Ь-іuldV >
> [|i lk-lvldVy\ (11.62)
Неравенства (11.58) и (11.62) позволяют получить строгие двусторонние оценки для коэффициентов продуктивности без фактического решения задачи (11.37) — (11.38). Чтобы сделать это, нужно взять произвольные пробные поля <ро и vo, удовлетворяющие условиям Д<ро = li Q [©о] = 1> div Vo = 0, и вычислить для них интегралы - ЛЫ И /3[Фо]. Тогда
H [©о] < Л < /і [еро]. (11.63)
Насколько удовлетворительной будет такая оценка, зависит от того, как удачно выбраны пробные функции <ро и ©о. Ниже приведем примеры использования этого подхода для оценки дебитов скважин.
Вопрос об оценках коэффициентов продуктивности можно поставить и по-другому. Если область D имеет сложную форму и (или) распределение проницаемостей в ней является достаточно сложным, естественно ставить вопрос о том, что будет с дебитом (или коэффициентом продуктивности), если изменить форму области и (или) распределение проницаемости. На этом пути удается получить простые и вместе с тем важные вариационные оценки. Докажем, прежде всего, физически ясное утверждение, что если при фиксированной форме трубки тока и граничных условиях изменим поле проницаемостей k таким образом, что в каждой точке она не уменьшится (т. е. либо увеличится, либо останется прежней), то при том же перепаде фильтрационный расход не уменьшится. Формально это сводится к тому, что рассматривается коэффициент продуктивности Л как функционал от формы области D и от распределения в ней проницаемости и показывается, что этот функционал является монотонным по k:
Л = Л [D, k], Лі = Л [D, Л,], (11.64)
Л > Ль если k(M) > k\ (М), для всех M^D. Действительно, пусть {р, и} — решение, отвечающее распределению проницаемостей k, а [ри U\)—решение, отвечающее распределению k\. Имеем:
Лі = [pi, kx] < 2p-iP-2Y* [p, k\] =
= jji-'P-2^! І у/? 12dV < Ik I VP \2dV =
D D
= 2^P-2Y* [p, k] = Л. (11.65)
При этом первое из неравенств (11.65) следует из того, что pi минимизирует функционал Y* [<?, k\\, а второе — просто из того, что k > kl.
В частности, при введении в область течения непроницаемых перегородок коэффициент продуктивности будет уменьшаться, а при введении областей бесконечной проницаемости — увеличиваться.
Разобьем поток тонкими непроницаемыми поверхностями на множество тонких трубок тока, таких, что течение в каждой из них можно считать одномерным. (Это эквивалентно заданию направления линий тока в каждой точке пласта.) Тогда по доказанному подсчитанный таким образом коэффициент продуктивности окажется меньше действительного.
Напротив, если зададим форму поверхностей постоянного давления (изобар) (что эквивалентно введению в поток множества бесконечно тонких поверхностей бесконечной проницаемости), то рассчитанный таким образом коэффициент продуктивности окажется завышенным по сравнению с действительным (см. пример 3).
Еще одно важное утверждение получим следующим образом. Выберем вблизи непроницаемой (боковой) границы области течения примыкающую к ней подобласть Dc и будем уменьшать проницаемость в ней до нуля. В пределе будем иметь новую область течения с вырезанной подобластью DЈ (с вдавленной границей). По доказанному ранее коэффициент продуктивности уменьшится.
С другой стороны, если область Dt примыкает к одной из изобар — входной С і или выходной Сг — и проницаемость в ней стремится к бесконечности, то в пределе получим область со вдавленной внутрь входной или выходной границей. По доказанному ранее коэффициент продуктивности при этом увеличится.
Таким образом, имеем так называемый принцип в дав - лив а н и я. При «вдавливании» в область фильтрации непроницаемых границ коэффициент расхода уменьшается, при вдавливании» входной и выходной изобар коэффициент расхода увеличивается. Отсюда уже непосредственно получаем принцип сравнения областей: если входная изобара Сі (контур питания) для области D может быть заключена между входными изобарами для областей D* и Dt, D^aDczD*, то коэффициент продуктивности для области D принимает промежуточное значение между коэффициентами продуктивности для областей и D*:
Л*<Л<Л,. (11.66)
Для однородных областей (k = const) ряд оценок можно получить, используя так называемые теоремы о симметризации. Известно [32], что если область D подвергается симметризации (относительно плоскости, прямой, точки) или последовательности отражений, то уменьшается интеграл f | yep \2dV. Отсюда следует, что симметри-
Ъ
Зация области движения приводит к уменьшению коэффициента продуктивности (см. пример 4).
Можно рассмотреть и более общий вопрос о пределах изменения коэффициента продуктивности области, если объем ее фиксирован. Поскольку ясно, что, сближая входную и выходную изобары, можно, не уменьшая объема области, получить сколь угодно большой расход, очевидно, что верхней границы для коэффициента продуктивности не существует. Однако существует нижняя граница. Одна из возможных при этом постановок задачи состоит в следующем. Рассмотрим бесконечную трубку Cq и пересекающую ее поверхность С2. Поставим задачу об определении такой поверхности С\, отсекающей вместе с поверхностями С2 и Cq область D заданного объема V, чтобы коэффициент продуктивности этой области (при входе Сь выходе С2 и непроницаемой границе Cq) был минимален.
Оказывается [17], что на искомой границе Сі должно выполняться дополнительное условие постоянства потока: и„ = const. Для однородного пласта это позволяет в явном виде сформулировать и решить задачу отыскания области минимального расхода.
Пример 1. Пусть задан горизонтальный пласт постоянной мощности с кон" туром питания С, на котором поддерживается постоянное давление Р0, и с п эксплуатационными скважинами радиусов гк, помещенными в точках гк(хк, ук). По технологическим соображениям для каждой скважины устанавливается некоторое минимальное допустимое значение забойного давления Р~. Требуется так выбрать забойное Давление Рк из допустимого диапазона для каждой скважины
Р7<Рк < р0>
Чтобы суммарный дебит скважин Q был максимальным.
Прямое решение этой задачи требует достаточно сложных расчетов. Вначале следовало бы, решая задачу напорной фильтрации для области со скважинами, найти зависимость дебитов от забойных давлений:
<2/= £ ли(Р0-Рд,
Где Аи—матрица коэффициентов влияния, а затем максимизировать сумму
£<3.= t Aik{po-pi) k=\ і, k=l
С учетом ограничения (11.67).
На самом деле во всем этом нет необходимости. Основываясь на принципе максимума, можно показать, что максимальный суммарный дебит достигается при минимальных допустимых забойных давлениях.
Действительно, пусть р0(х, у) — решение задачи напорной фильтрчции, отвечающее граничным условиям р0 | Ск = Р~, а р (х, у) — решение для другого набора значений давлений на скважинах Рк, удовлетворяющего условиям (11.67).
Составим разность р (х, у) = р — Ро - Так как задача напорной фильтрации линейна, р — решение, которое на контуре питания С0 обращается в нуль, а на контурах скважин Ск принимает положительные значения. По принципу максимума во всей области фильтрации
Р(х, у) > 0 = minp {С0, С,, ..., Ск, . . ., Сп}.
Отсюда и из условия на контуре питания р0 = 0 находим, что на контуре питания др/дч > 0, где ч — направление внутренней нормали. Следовательно, "»— "ov = — (др/дч — др0!дч) < О,
Q = 5 u, dS < Q0 = ; u0,dS. с с
Это и доказывает сделанное утверждение.
Пример 2. Рассмотрим скважину радиуса р, центрально расположенную в круговом пласте радиуса R. Допустим, что эта скважина окружена зоной с проницаемостью k*<k. Попытаемся оценить, как это повлияет на дебит скважины.
Обозначим через г_ и максимальное и минимальное расстояния от центра скважины до границы зоны ухудшенной проницаемости. Дебит скважины оказывается заниженным, если считать зону измененной проницаемости кругом радиуса r_р и завышенным, если принять радиус зоны равным г_. Таким образом,
Q+< Q < Q_; Q± = 2-kh (Рк - Pc) (Л-1 (In R! r± + k/k_ In r±/f). (11.67)
Фактически, если размер загрязненной зоны составляет несколько метров, а г_ и отличаются в несколько раз, правые и левые части неравенства (11.67) близки между собой. В результате оказывается излишним детальное исследование влияния формы зоны на величину дебита.
Пример 3. Рассмотрим пласт, имеющий форму равнобедренного треугольника ABC, в вершине А которого с углом а расположена скважина радиусом р. Допустим также, что стороны АВ и АС непроницаемы, а основание ВС является изобарой («контуром питания»). Для оценки дебита скважины примем сначала, что пласт разбит прямолинейными границами на узкие секториальные трубки тока. Суммируя их дебигы, получим
Q = <?_ = f^rin-^l-1d? = 2i^f[ln-^-lncosJ~V (11.68)
J [х L р cos cpJ (j. J 1 r1 J
Затем, разбивая пласт на тонкие слои концентричными со скважиной изобарами, получим
Q = Q+; Ар = Q+ Q+ = (11.69)
+ ^ J 2khi г ^ ц In (Rlp)
P
По доказанному, для истинного дебита Q имеем 0_ < Q <
Г In cos 01—1 1 с г In cos ч>і—I iiQ R
І'-щщ] <7І[1-|Щ-] (IL7°)
О
Достаточная для технических расчетов 10 %-ная точность заведомо сбеспечи - вается при R/р = 100 вплоть до а =0,9 = 51°.
Пример 4. Допустим, что имеется плоский пласт площадью S с контуром питания С и с круговой галереей радиусом р < R = (S/п)1^2.
Выполняя симметризацию относительно оси галереи, получим задачу о течении между двумя круговыми галереями радиусов р и R. По сказанному выше, для дебита исходной задачи имеем