АППАРАТЫ ХИМИЧЕСКОЙ ТЕХНОЛОГИИ
Опытные данные по теплоотдаче
Для исследования процессов конвективного теплообмена проведено огромное количество опытов. Путем обработки опытных данных с применением теории подобия получены уравнения и формулы, которыми пользуются в практических расчетах по теплопередаче.
В формулах, приводимых ниже, приняты следующие обозначения: w—скорость в м/сек\ j—уд. вес в кгс/м3',
Ср—удельная теплоемкость при постоянном давлении в ккал/кгс-°С; к—теплопроводность в ккал! м-час-°С; Л. О g—ускорение силы тяжести в м/сек2-, р—плотность в кгс-сек2/м*\ jx—вязкость в кгс - сек/м2\
20*
Г—скрытая теплота конденсации в ккал/кгс\ I—линейный размер в місі—внутренний диаметр трубы в ж; dH—наружный диаметр трубы в м; t—температура в °С; Т—температура в °К; L—длина трубы в м.
Коэффициент теплоотдачи при вынужденном турбулентном потоке в прямой трубе круглого сечения. В общем виде уравнением теплоотдачи при вынужденном турбулентном потоке является выражение
Nu = f(Re, Prf-j~) \ '»/
Обработкой опытных данных исследователи получили различные расчетные формулы. Наиболее надежные результаты дает следующая формула, применимая как для капельных жидкостей, так и для газов
Nii = 0,022>Re0'8Pr°-* (2—46)
Из которой следует:
А = 0,023-i Re°'8Prккалім2« час• °С (2—46а)
Формула (2—46а) применима при следующих значениях: критерий /?е>10 000, критерий Рг=0,7-^-2500, температура стенки—ниже температуры кипения жидкости, отношение длины трубы к ее диаметру—
Для коротких труб среднее значение коэффициента теплоотдачи получается несколько выше; при -^-=30-^-40 это увеличение не превышает 2—7%,и лишь для очень коротких труб приобретает существенное значение*.
Значения физических констант принимаются при средней логарифмической температуре жидкости.
При турбулентном режиме движения величина теплоотдачи зависит и от направления теплового потока. Исследованиями показано, что изменение физических параметров жидкости неодинаково при ее нагревании и охлаждении.
По В. Н. Тимофееву
Nu = ARe°<*Prn
Где Л=0,021 и п—0,45 при^нагревании жидкости; Л=0,026 и л=0,35 при ее охлаждении.
Однако до уточнения указанной зависимости в технических расчетах можно * пользоваться формулой (2—46).
Коэффициент теплоотдачи при переходном режиме движения. В области значений критерия Re=2300—10 000, т. е. в переходном режиме, коэффициент теплоотдачи зависит от критерия Рейнольдса в большей мере, чем при устойчивом турбулентном движении жидкости. Для вывода количественных зависимостей еще не накоплено достаточно экспериментальных данных. В первом приближении значение а можно
Принимать равным полученному по формуле (2—46а) и умноженному на поправочный коэффициент /; числовое значение этого коэффициента
/ = (1 -5- 6). КР/йг-ьв. (2—47)
Коэффициент теплоотдачи при вынужденном ламинарном потоке в прямой трубе круглого сечения. В данном случае следует учитывать зависимость теплоотдачи от естественной конвекции жидкости, а также направления теплового потока.
Для горизонтальных труб наиболее точные результаты дают формулы [при (Re Rr)> 18001:
Nu » 0,74 (Re - Pr)0-2 (Gr • Рг)0[3] (2—48)
И
А = 0,74 A (Re-Pr)0-2 (Gr-Рг)0-1 (2—48а)
Для вычисления критерия Грасгофа принимают Дt равной разности между температурами жидкости и стенки. Значения физических констант принимают при среднеарифметической температуре жидкости и стенки
Определяющим линейным размером является d—диаметр трубы.
Для коротких труб при Ш<50 величина коэффициента теплоотдачи будет больше полученной по формуле (2—48). При lid—40 она больше на 5%, при ltd—30 больше на 13% и значительно увеличивается при дальнейшем уменьшении отношения lid*.
Для вертикальных труб величина коэффициента теплоотдачи зависит от взаимного направления вынужденного потока и свободного движения жидкости. При совпадении их направлений, т. е. в случае если жидкость при нагревании движется снизу вверх, коэффициент теплоотдачи можно принимать равным 0,85а, где а—коэффициент теплоотдачи, вычисленный по формуле (2—48а); при несовпадении указанных направлений коэффициент теплоотдачи равен 1,15 а.
Коэффициент теплоотдачи в трубе любой формы сечения. Если труба имеет сечение не цилиндрическое, а любой другой формы, то, определяя коэффициенты теплоотдачи при вынужденном потоке капельной жидкости или газа, необходимо вместо диаметра d подставить соответствующий «эквивалентный» диаметр. Обозначим:
F—площадь поперечного сечения трубы в м2; 77—часть контура, участвующего в теплообмене, в м. Тогда величина «эквивалентного» диаметра d9KB. будет, как указывалось выше
D = •^ЭКВ. [J
В частных случаях можно более точно определить коэффициент теплоотдачи. 1. Труба кольцевого сечения.
/ D \о.«
Nu = 0,023 I D_D) Re*.*Pt*'* (2—49)
\ I D \o.45 Ккал N Л
A-°>023d(D=d) (2-49a>
Где, кроме предыдущего,
D—наружный диаметр внутренней трубы в м; D—Внутренний диаметр наружной трубы в м.
2. Пучок труб внутри цилиндра.
В случае продольного движения теплоносителя в межтрубном пространстве коэффициент теплоотдачи может быть определен по приближенной формуле
Nu — 1,1Re0 • ePr°'38
A = 1,16 -^-D^Re^Pr^
Где D3KB.—эквивалентный диаметр межтрубного пространства в м, отнесенный ко всему смоченному периметру; W—скорость в свободном сечении в м/сек. 3. Пучок труб внутри цилиндра с поперечными не Ре - Городками.
|
|
|
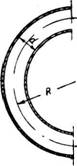
Рис. 208. Изогнутая труба. |
|
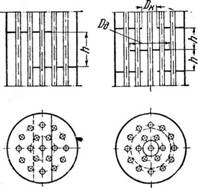
Рис. 207. Пучок труб в цилиндре: |
|
II |
/—с сегментными перегородками; II—с кольцевыми перегородками.
|
|
Поперечные перегородки в межтрубном пространстве могут быть сегментными (рис. 207,/) или в виде чередующихся дисков и колец (рис. 207, II).
В этом случае коэффициент теплоотдачи определяют по формуле
|
|
|
0.14 |
|
(2-51) |
Nu = CD°;LBReO'W'™
|
|
|
(2—51а) |
Гд X /їх \0,14
Где С= 1,72 для сегментных перегородок и С=2,08 для кольцевых;
|
(2—52) |
W—скорость жидкости в м/сек, определяемая по эффективному сечению. Эффективное сечение может быть определено по формуле
Fe — попер.' /прод.
|
|
/попер. —площадь свободного сечения для прохода жидкости при поперечном обтекании пучка труб в м2; /прод. —площадь свободного сечения отверстия перегородки (площадь сегмента или выреза в кольце) минус суммарная площадь сечения проходящих через него труб в м2.
|
Где |
Для сегментных перегородок
|
|
|
(2—53) |
|
Т) |
= Л£> 1 —
Попер.
|
|
-расстояние между перегородками;
|
Где |
-шаг перегородок в направлении, перпендикулярном потоку.
Для перегородок в виде чередующихся дисков и колец
/попер. = NDCp.H ^ 1 — - у-^ (2—53а)
DK-\-Dd
Где DCp = 2 (см. рис. 207).
Для подстановки в формулы (2—49а), (2—50а) и (2—51а) принимают физические константы при средней температуре жидкости.
Коэффициент теплоотдачи в изогнутой трубе. При протекании жидкости в изогнутой трубе, например в змеевике, происходит усиление турбулентности потока под действием центробежных сил, и в поперечном сечении такой трубы (рис. 208) всегда возникает дополнительная, вторичная циркуляция жидкости.
Коэффициент теплоотдачи для змеевиков может быть приближенно определен по уравнению
Clr = ос 1,77 ~ j (2-54)
Где а—коэффициент теплоотдачи для прямой трубы;
D—диаметр трубы в м;
R—радиус кривизны змеевика в м.
Обычно увеличение ос вследствие изгиба трубы незначительно.
Коэффициент теплоотдачи для жидкости, перемешиваемой механическими мешалками. Если жидкость приводится в движение при помощи механической мешалки, то величина коэффициента теплоотдачи зависит от формы поверхности нагрева, размеров лопастей мешалки и числа ее оборотов. Так как при размешивании турбулентность движения жидкости значительна, то уравнением теплоотдачи в общем виде будет
Nu ~CRemPrn (А)
• Как указывалось в гл. VI, для процессов перемешивания жидкости критерию Рейнольдса придают несколько иной вид, вводя вместо скорости число оборотов мешалки. Как известно, скорость и число оборотов связаны между собой зависимостью
W = It Dn
Где w—скорость вращения мешалки в м/сек; d—диаметр лопасти мешалки в м; п—число оборотов мешалки в сек.
При таком преобразовании критерий Рейнольдса принимает виД
|
\0,14 |
= WdP = D2NP
Причем постоянная величина ir учитывается в коэффициенте пропорциональности С уравнения теплоотдачи (А).
Если теплообмен с перемешиваемой жидкостью происходит через рубашку, то можно принять
2 1
Nu = 0,36Яет Рг*( —^—У V Не Т. I
Или
2 1
А =0,36 ~ ReЈ Рг ^ (——)014 ккал! м2■ час• °С к 2-55)
D и ^ j
Где, кроме известных величин, принято: D—диаметр аппарата в м;
Jj.—вязкость жидкости в кгс-сек/м2 при средней температуре стенки
У _1_f
И ЖИДКОСТИ ^ср.= 2 Ж»
Fj. CT.—вязкость жидкости при температуре стенки (рубашки) в кгс-сек/м2.
Если теплообмен с перемешиваемой жидкостью происходит через змеевик, то уравнение теплоотдачи имеет вид:
Nu = 0,87ReJ>-«2pA /_іі-Л0Л4
\ {%Г. /
ИЛИ
А— 0,87~ReM0,62Pr~^ккал/м2-час-°С (2-56)
Где все обозначения те же, что и в уравнении (2—55).
Значения физических констант р, ср и X в уравнениях (2—55) и (2—56) принимают при средней арифметической температуре жидкости.
Формулы (2—55) и (2—56) выведены для аппаратов диаметром до 300 мм; для аппаратов большего диаметра они дают завышенные результаты.
Коэффициент теплоотдачи при вынужденном поперечном потоке жидкости относительно одиночной трубы. Для капельных жидкостей коэффициент теплоотдачи может быть определен из уравнения
Nu = CRenPr°(2—57)
Или
« = С ~ RenPr°-4 (2—57а)
Аи
Где С и п—коэффициенты, зависящие от величины критерия Re (табл. 14).
Таблица 14
|
Значения коэффициентов Сип
|
Физические константы в формуле (1—57а) определяют при средней температуре жидкости; в качестве определяющего линейного размера следует принимать наружный диаметр трубы dH.
Для газов одинаковой атомности критерий Прандтля является величиной постоянной и формула (2—57) может быть в этом случае упрощена путем исключения множителя Рг0'4. Значения коэффициентов п и С для газов (в скобках) также приведены в табл. 14.
Коэффициент теплоотдачи при вынужденном поперечном потоке жидкости относительно пучка труб. Теплоотдача поперечного потока жидкости, омывающей пучок труб, может быть определена по формуле
Nu = CeRenPr0'* (2—58)
Причем значения ей п зависят от расположения труб в пучке и порядкового номера ряда их по глубине пучка.
При коридорном расположении труб (рис. 209, /) для первого ряда п=0,6 и в=0,171, второго, третьего и четвертого рядов л=0,65 и є=0,157. При шахматном расположении труб (рис. 209, II) для всех рядов п—0,6; причем для первого ряда є=0,171, для второго е=0,228, для третьего и четвертого рядов є=0,29.
Числовое значение коэффициента С зависит от отношения шага трубы к ее диаметру Sх!& (рис. 209): при SJd= 1,2-^-3 C=l+0,lS1/d и при St/d>3 С= 1,3. *
Формула (2—58) применима ^Sg-^-Sg-^. r-^-i-J^
Для круглых труб в пределах значе - ^ ^ ний Яе=5000-70 000 и SJd= ^ Д/^ А ^
TOC \o "1-3" \h \z =SJd= 1,2-5. ±0- W -0 -Fa Ф
Значения физических Констант ——-ф - В формуле (2—58) принимают по -0 -0- -0 -0- 0-
Средней температуре жидкости, а рядь, 12 3 12 3
Скорость потока—для самого узкого
Сечения в пучке. Следует, однако, ^ В
Учесть, что для капельных жидкостей
Этот случай теплообмена почти не рИс. 209. К определению коэффициента исследован, И поэтому формула теплоотдачи при поперечном обтекании (2—58) пригодна только для ориен - пУчка ^У6-
Тировочных расчетов.
Для воздуха и дымовых газов подробные исследования были проведены В. М. Антуфьевым, JI. С. Козаченко, Н. В. Кузнецовым и др. Результаты этих исследований могут быть выражены следующей степенной зависимостью:
Nu = Ce'Ren ' (2—58а)
Причем при коридорном расположении труб для первого ряда г =0,15 и для второго, третьего и четвертого рядов є'=0,138. При шахматном расположении труб для первого ряда е'=0,15, для второго є'=0,20, для третьего и четвертого рядов є'=0,255. Остальные величины те же, что и в формуле (2—58).
Формулы (2—58) и (2—58а) применимы при движении потока перпендикулярно оси пучка, т. е. когда так называемый угол «атаки» ф=90". Если угол ф<90®, то значение коэффициента теплоотдачи, полученное по указанным выше формулам, следует умножить на поправочный коэффициент <р.
Ниже приведены значения коэффициента <р (по исследованиям В. А. Локшина И JI. П. Орнатского) для газов при коридорном и шахматном расположении труб:
.... 90 80 70 60 50 40 30 20 10 <р 1 1 0,98 0,94 0,88 0,78 0,67 0,52 0,42
Коэффициент теплоотдачи при свободном движении жидкости.
При свободном движении жидкостей, т. е. движении, обусловленном различной плотностью их нагретых и холодных частиц, применимо критериальное уравнение (2—436)
J______ In
'о ^о
Результаты исследований, проведенных с жидкостями, смачивающими стенку, для которых критерий Рг>0,7, были обобщены М. А. Ми - хеевым, причем им установлена следующая зависимость:
Nu С (Gr-Pr)n (2—59)
|
Nu — F (Gr, Pr, |
Исследования показали, что свободное движение жидкости имеет три режима: ламинарный, переходный (локонообразный) и вихревой. Преобладание того или иного режима зависит от А/—разности температур
Поверхности теплообмена и жидкости, а также от формы и величины поверхности.
Значения коэффициентов Сип изменяются в зависимости от режима свободного движения жидкости (табл. 15).
Таблица 15
|
Значения коэффициентов С и /г
|
Выразим в уравнении (2—59) критерии Nu, Gr и Рг через составляющие их величины и подставим соответствующие значения коэффициентов Сип. Тогда получим для труб и вертикальных плит следующие выражения коэффициентов теплоотдачи: при Gr-Pr=5-Ю2—2-Ю7
А = 0,54 А ^ ккал/м2-час-°С (2—60)
Или
Зі і
А — 13,1 • (2—60а)
При Gr-Рг>2-107
А = 0,135 P2[jA^T(36Q0f';"g )~3~ ккал/м2-час-°С (2—61)
Или
— хЛ
А - 9,48 (Хр) з / FcpMJs - (2—61a)
Где Р—коэффициент объемного расширения В А;
Ы—разность температур стенки и жидкости в °С; I—определяющий линейный размер в м.
Значения физических констант для подстановки в уравнения (2—60) и (2—61) принимают при средней температуре стенки и жидкости, = 0,5 (/„.+/«).
При Gr-Pr>2-107 процесс теплообмена автомоделей, т. е. не зависит от геометрических размеров поверхности теплообмена.
Приведенные выше формулы относятся к теплоотдаче в неограниченном пространстве. В случаях естественной конвекции в ограниченном и замкнутом пространстве (каналах, рубашках и т. п.) процесс теплоотдачи осложняется, так как на него влияет величина и форма пространства. В этом случае для упрощения расчетов принимают, что теплообмен происходит путем теплопроводности, причем вводят понятие эквивалентного коэффициента теплопроводности:
^экв. = К (2-62)
Где - X.—коэффициент теплопроводности жидкости в ккал! м-час-°С\ ек—коэффициент, учитывающий влияние конвекции. Значение коэффициента конвекции ек можно приближенно определить по формуле
1
Ек = 0 ,Щвг-Рг)* (2—63)
В качестве определяющей температуры в уравнениях (2—62) и (2—63) принимают среднюю температуру жидкости: ^ж=0,5(/ст.1-|-^ст.2).
Коэффициент теплоотдачи при стенании жидкости пленкой по вертикальной по верхности. Рассмотренные выше формулы относились к случаю, когда жидкость заполняет все сечение трубы. Если жидкость стекает в виде пленки по вертикальной поверхности, в частности по внутренней поверхности трубы, то коэффициент теплоотдачи может быть определен по следующим формулам: при турбулентном стекании пленки
А = 0,01 -Jr- (Re.Pr.Ga)3 ккал/м2-час°С (2—64)
При ламинарном стекании пленки
І І - - -
А = 0,67 Re3 Рг 2 Са 9 ккал/м2»час.°С ' (2—65)
Безразмерные критерии, входящие в уравнения (2—64) и (2—65), имеют сле - 4 U*
Дующие значения: Re= ——, где и—плотность орошения в Кгсім. сек, Т. е. ко-
И є
* D 3600cPpg Личество жидкости, орошающей 1 м периметра трубы в сек.; Рг» ------ ^—;
^ л/ ah и
Оа и Nu= -у, где h—высота поверхности.
Значения физических констант принимают при средней температуре пограничной пленки: tCP.=0,5(tx-\-tCT.).
Критическое значение критерия Re, Соответствующее переходу ламинарного движения пленки в турбулентное, равно 2320.
Коэффициент теплоотдачи при вынужденном потоке газа вдоль плоской стенки. Если теплопроводящие стенки состоят из плоскостей, находящихся на небольшом расстоянии друг от друга, тем самым образуя. замкнутые каналы, то процесс теплообмена можно рассматривать как теплообмен в трубе прямоугольного сечения.
Если же слой газа, протекающего вдоль плоской стенки, велик, то рассмотренные выше формулы теплообмена в трубе - неприменимы и приходится выводить специальные формулы теплоотдачи от плоских стенок.
Коэффициент теплоотдачи в этом случае можно приближенно определить из рчедующей зависимости:
Nu = 0,0356Re°'8Pr^ (2—66)
Откуда
А = 0,0356 - j #e0-8Pr0'4 (2—66a) где I—длина стенки в м и Re
W.D9 Kb.Y Ссек. . 4/
---- №------- ' Н° F— "экв. = ~хГ
Отсюда
Г, Ссек.'4/ 4Ссек. __ 4U
Физические константы, входящие в уравнение (?—66), принимают при средней температуре жидкости.
Коэффициент теплоотдачи при конденсации паров. Конденсирующийся пар может осаждаться на поверхности охлаждающей стенки в виде капель или пленки. Конденсация первого вида называется капельной, а второй—п леночной. Капельная конденсация обычно происходит в том случае, когда поверхность охлаждения не смачивается конденсатом, что наблюдается при конденсации на хорошо отполированной поверхности пара с примесью масла, керосина, жиров, или при конденсации чистого пара на полированной поверхности, покрытой тонким слоем этих веществ.
Пленочная конденсация происходит при однородных парах и чистых поверхностях охлаждения, которые полностью смачиваются жидкостью. Коэффициент теплоотдачи при пленочной конденсации значительно ниже, чем при капельной. На практике оба вида конденсации обычно встречаются одновременно.
Теория пленочной конденсации заключается в следующем.
При быстрой конденсации пара на вертикальной стенке вследствие разности температур пара /нас. и стенки tcТ>1 образуется сплошная пленка жидкости; под действием силы тяжести, которая направлена параллельно стенке, конденсат стекает вниз, причем толщина его слоя постепенно увеличивается вследствие добавления новых количеств конденсата.
Средняя скорость стекания конденсата зависит от его удельного веса (у) и внутреннего трения или вязкости] (ja). Оба эти параметра зависят от температуры.
Температура жидкой пленки принимается равной с одной ее стороны ^ст. і, а с другой—температуре пара 4ас..
Если движение пленки ламинарное, то количество тепла, проходящее через нее, может быть определено по уравнению теплопроводности.
Q = X-------- G------ - Fx ккал
Где 5—толщина пленки.
Это же количество тепла можно выразить общим уравнением теплоотдачи
Q = a (tHaC. — 4т. і) Fx Ккал
Приравняв оба уравнения, получим
X
А = —- о
Таким образом, коэффициент теплоотдачи ос целиком зависит от толщины слоя конденсата Ь, стекающего по стенке, и чем толще этот слой, тем меньшей будет теплоотдача.
—' Разобрав термические и гидродинамические условия образования пленки конденсата, Нуссельт вычислил ее толщину и затем, интегрируя количество тепла, проходящего через пленку данной высоты, определил теоретически величину коэффициента теплоотдачи от пара, конденсирующегося на вертикальной стенке. При этом им не была учтена турбулентность движения пленки и физические параметры приняты постоянными. ~ Лучшее совпадение с данными опытов дают величины коэффициентов теплоотдачи, вычисленные по формулам, полученным на основе приложения теории подобия к теплообмену при конденсации паров.
Где г—скрытая теплота конденсации в ккал/кгс;
С—теплоемкость в ккал /кгс -°С;
Дt=tHac.—іСТш1—разность между температурами пара и стенки.
Критерий конденсации К является определяющей величиной во всех случаях теплообмена, связанных с изменением агрегатного состояния вещества.
Общая связь между критериями подобия для теплообмена при конденсации пара представляется в следующем виде:
Nu = F{Ga, Рг, К)
Из опытных данных С. С. Кутателадзе, при ламинарном течении пленки конденсата (і? ек<180) коэффициент теплоотдачи при конденсации пара на вертикальной трубе может быть определен по уравнению
«=1.15У (2-67)
F п (/нас. [ст. і)ім
Где К т и и—теплопроводность, удельный вес и вязкость конденсата, определяемые при средней температуре пограничной пленки tcp. =0,5(^нас.+іст.1). Скрытая теплота конденсации пара г определяется при температуре насыщения /нас..
Если і? ек>180, то в нижней части трубы пленка конденсата движется турбулентно и коэффициент теплоотдачи равен
А 0,107 \Pr yijrf (2—67a)
Значение ReK находят по уравнению
Г) А(^нас. TCT.)/I
Для расчета величины коэффициента теплоотдачи при конденсации пара на горизонтальных трубах следует пользоваться формулой (2—67), но вместо коэффициента 1,15 брать коэффициент 0,725 и вместо высоты стенки h в качестве определяющего геометрического размера принимать наружный диаметр трубы dH.
При конденсации пара на пучке горизонтальных труб вместо d следует подставлять в формулу сумму наружных диаметров труб, расположенных друг над другом s = гДе п—общее] число труб, a m—
Число рядов труб по вертикали.
Когда насыщенный пар содержит воздух и газы, коэффициент теплоотдачи значительно уменьшается, так как у стенки скапливается воздух, образующий своего рода воздушную прослойку, через которую молекулы пара движутся лишь путем диффузии.
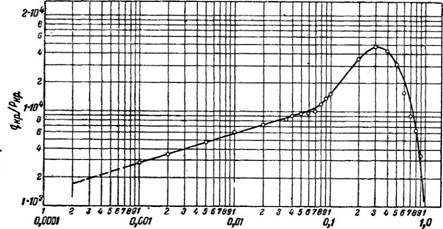
Точных методов расчета теплоотдачи от паро-газовых смесей не имеется. Для ориентировочных расчетов при любом содержании воздуха в паро-воздушной смеси можно пользоваться графиком (рис. 210).
|
В данном случае изменение состояния на границе перехода паровой фазы в жидкую учитывается введением критерия конденсации: |
![]()
Коэффициент теплоотдачи при кипении жидкости. Теплоотдача при кипении жидкости является весьма сложным процессом. Опыт по-
называет, что характер протекания этого процесса и его интенсивность зависят от разности температур поверхности стенки, отдающей тепло tcrи образующегося при кипении пара tHaCm. Эта разность температур М= =/ст.—tHac. будет тем больше, чем больше удельная тепловая нагрузка поверхности нагрева
Q = = c/At ккал/м2- час
При небольших удельных тепловых нагрузках ^<5-103 ккал/м2-час образование пара на обогреваемой поверхности происходит лишь в отдельных ее точках (мельчайшие бугорки на шероховатой поверхности, загрязнения и т. п.), называемых центрами парообразования.
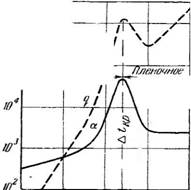
|
OJ / Ю Ю' /0S |
|
Рис. 211. Зависимости а и Q От At Для воды. |
|
Пузырчатое |
|
Кипение |
|
Ншение |
|
О /О го 30 40 50 Б О 70 80 SD /00 Среднее содержание пара в смеси по объему,.% Рис. 210. График для определения коэффициента теплоотдачи от паро-газовых смесей. |
|
8 ' !! Is0 И Iі- М |
|
|
С возрастанием At или повышением давления число центров парообразования увеличивается, и кипение становится более интенсивным. Если кипение жидкости происходит в большом объеме при малых значениях t\t, а следовательно, при небольших удельных тепловых нагрузках, то процесс теплоотдачи определяется в основном естественной конвекцией и коэффициент теплоотдачи а можно приближенно определять по уравнениям (2—60) и (2—61). При атмосферном давлении уравнения естественной конвекции применимы при разности температур Д£<5° и тепловых нагрузках ^<5-103 ккал/м2-час.
С возрастанием удельной тепловой нагрузки интенсивно образующиеся пузырьки пара способствуют увеличению скорости движения жидкости; коэффициент теплоотдачи при этом увеличивается. Режим кипения в таких условиях называют обычно пузырчатым или" ядерным. При дальнейшем увеличении разности температур между стенкой и кипящей жидкостью образующиеся пузырьки пара сливаются между собой и на поверхности теплообмена создается сплошная пленка пара; при этом коэффициент теплоотдачи резко уменьшается. Режим кипения в таких условиях называют пленочным.
Значения удельной тепловой нагрузки, разности температур и коэффициента теплоотдачи, соответствующие переходу ядерного режима - кипения в пленочный, называют критическими. Очевидно, оптимальным режимом кипения жидкостей является режим ядерный, приближающийся к критическому.
Для воды при атмосферном давлении зависимости q— f(kf) и а=«р(Дt} представлены на рис. 211.
Коэффициент теплоотдачи для воды при кипении ее в условиях ядерного режима, наличии только естественной циркуляции и при давлениях от 0,2 до 100 ата можно определить по одной из двух формул:
Ссв == 2,53Р0-171У-7 ккал/м2-час°С (2—69)
И
Ссв=22Я0'58Дга.зз ККал/м2-час-°С (2—69а)
Где Р—давление в am;
Q—удельная тепловая нагрузка в кшл! м2-час\ 4т.——разность температур в °С.
Определение коэффициентов теплоотдачи для любых других жидкостей и особенно растворов значительно сложнее. Разные исследователи, пользовавшиеся общим методом теории подобия, предложили формулы для определения коэффициентов теплоотдачи для различных жидкостей, однако эти формулы исключительно сложны по количеству входящих в них физических констант, а получаемые результаты во многих случаях не обеспечивают достаточную для практических расчетов степень точности.
Весьма оригинально и относительно просто с достаточной степенью точности можно определять коэффициент теплоотдачи при кипении любой жидкости и раствора, пользуясь методом, предложенным А. И. Рычковым.
А. И. Рычков предложил для выражения теплообмена при кипении жидкостей и растворов следующие критериальные уравнения: для чистых жидкостей и их смесей
Для растворов
В этих уравнениях:!
Es—эбулиоскопический критерий; q—удельная. тепловая нагрузка в ккал! м2-час\ Якр.—критическая удельная тепловая нагрузка в ккал/м2-час; <7кр. Ус.—условная критическая удельная тепловая нагрузка в ккалім2; Р—давление пара, образующегося при кипении в ата; Ркр.—критическое давление для данной жидкости в ата; Росм.—осмотическое давление в данном растворе при данной концентрации в ата\
Роем.—осмотическое давление в данном растворе при концентрации» соответствующей насыщенному раствору, в ата. Критическую удельную тепловую нагрузку можно находить из.
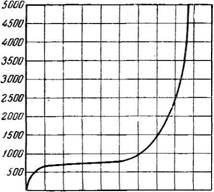
Зависимости a~p-=f[w~) по диаграмме, изображенной на^рис. 212.
" кр. ч*кр.'
Опытных данных по определению критической удельной нагрузки для растворов нет. Поэтому принимаем условно, что для растворов критическую удельную тепловую нагрузку можно определять так же,
Как и для чистых жидкостей по диаграмме, принимая вместо величину
<7ко vr Р - ГРрсм. <7 0 v ( Pqcm. \
-iSJiE: и вместо ъ—величину-^—, т. е. из зависимости =/ ( р* ,
Кр. Гкр. осм. ' кр. v осм./
Где Qкр. ус.—условно критическая удельная? тепловая нагрузка для раствора данной концентрации; Росм.—осмотическое давление раствора данной концентрации при температуре кипения и данном внешнем давлении, *
Роси. —осмотическое давление насыщенного раствора при температуре кипения и данном внешнем давлении.
|
Рис. 212. Зависимость J[ ) для кипящих жидкостей. Ркр - "Кр. ' |
При отсутствии опытных данных осмотическое давление может быть вычислено с большой точностью в кипящих даже очень концентрированных растворах как неэлектролитов, так и электролитов по формуле
(2-7!)
Где ДТ—температурная депрессия;
Т—абсолютная температура кипения раствора; г—теплота парообразования растворителя при температуре кипения его в ккал/кгс\ у'—удельный вес растворителя в кгс/м?.
Для определения осмотического давления при кипении насыщенного раствора Р*осм. можно пользоваться соотношением:
Р Р*
_= = const (2—71а)
AT * (АТ\* ГДЄ т= уИ т*= (yrj.
Эбулиоскопический^критерий Es представляет собой комплекс:
Е (2-72)
5 я
Где q—удельная тепловая нагрузка в ккал/м2-час\ а.—коэффициент теплоотдачи в ккал/м2- час - °С;
£__эбулиоскопическая постоянная растворителя, показывающая повышение температуры кипения, вызываемое растворением одного моля недиссоциирующегося вещества в 1000 г данного растворителя.
При отсутствии опытных данных эбулиоскопическую постоянную можно определять из уравнения
Е = W <2-73)
Где R—универсальная газовая постоянная, равная 1,986 в ккал! моль°К\ Т—температура кипения в °К; г—теплота парообразования в ккал/кгс.
При давлениях от 0,5 до 5 ата можно также для определения эбу - лиоскопической постоянной пользоваться уравнением
Е = 0,655- ЮТМ1-06 (2—73а)
Подставляя в уравнениях (2—70) и (2—70а) вместо Es его значение, находим выражения для определения коэффициента теплоотдачи при кипении:
Жидкостей
А =
Растворов
А = 0,095 4- М-Г" Г'6 (2—74а)
При этом показатель степени щ изменяется в пределах
П — 0,3]н-0,5
Уравнения (2—74) и (2—74а) относятся к теплоотдаче в условиях ядерного режима кипения, т. е. в пределах 5°<Л/<Л/1ф>.
Критическая разность температур определяется для жидкостей по уравнению
(2—75)
Для растворов выражение критической разности температур еще не найдено.
Коэффициент теплоотдачи при непосредственном соприкосновении потоков. В этом случае коэффициент теплоотдачи является и коэффициентом теплопередачи,* т. е. а—К. Для случая охлаждения воздуха водой в насадоЧном скруббере? Жаворонков и Фурмер дали обобщенную формулу
А = К = 0,01 RfMRetgPtКкал/м2■ час• °С (2—76)
Где Хг—теплопроводность газа в ккал! м - час - С;
4V
D9Kв.—эквивалентный диаметр—для насадки d3KB. = —^м (VCB.—
Свободный объем насадки в м3/м3\ а—удельная поверхность насадки в м2!м3);
—КрИтерИд Рейнольдса для газа (&уф—скорость газа фиктивная,
Wrg
Отнесенная к общему сечению аппарата, в м! сек\ уг—уд. вес газа в кгс! м3\ р. г—вязкость газа в кгс• сек! м2);
—критерий Рейнольдса для жидкости (Gx—плотность орошения
Скруббера в кгс! м2-сек\ р. ж—вязкость жидкости в кгс сек! м2).